Leer en 8 minutos.
Este texto fue lamido por 62 almas esta semana.
Entre un período de hospitalización en hospitales austriacos, un matemático llamado Kurt Friedrich Gödel provocó un desgarro tan profundo en nuestra comprensión de la realidad que todavía hoy sangra. El teorema de completitud de Gödel es la prueba lógica de que, en última instancia, tanto los científicos como los sacerdotes construyen castillos de ensueño sobre bases igualmente arbitrarias y que no existe ninguna posibilidad de que intenten siquiera demostrar que sus ilusiones son reales. No hay manera de confirmar si lo que ellos creen, o por extensión lo que tú crees, es real, correcto o al menos lógico.
La cosa funcionaría, de forma resumida y simplificada, de la siguiente manera:
Imagínate que estás leyendo esto justo antes del almuerzo, ese día que no pudiste desayunar ni comprar esos paquetes de galletas de R$ 1 para picar. El tiempo pasa y el hambre aumenta, hasta que empiezas a molestarte con esos carteles en las webs de compras colectivas que muestran macarrones, sushi y cortes de carne a medio cocer. En este momento, cuando el hambre se convierte para ti en una sensación física, te desafío: ¡demuéstrame que tienes hambre! Por supuesto que puedes decir "¡tráeme algo de comida y te lo mostraré!". Pero luego recuerdo ciertas veces que después de cenar alguien quiere salir a charlar e invariablemente la conversación se desarrolla en un restaurante o bar donde se piden raciones o platos, y aunque estaba satisfecho comí, y comí bien. También recuerdo a un sobrino que es capaz de comer feijoada hasta literalmente sentirse mal, para luego salir a pedir comida 15 minutos después porque tiene hambre. También recuerdo a una conocida que cuando tiene mucha hambre no puede comer nada porque siente malestar estomacal. Y respondo: comer no es prueba de hambre. Recuerdo a gente que come cuando está ansiosa, deprimida, feliz... y come con más ganas que un niño somalí comería un Big Mac. Si comer algo no es prueba de hambre, ¿cuál sería una buena prueba? ¿Pruebas para medir el azúcar en sangre? ¿Algún ejercicio físico para ver si presentas signos de debilidad? No todo esto podría dar resultados; de hecho, ciertamente daría resultados falsos positivos. Entonces intentemos algo diferente. Piensa en alguien a quien amas. Demuestra que realmente amas a esta persona. Opsss… el mismo problema, de la misma manera que no podemos usar el hambre para justificar el hambre, no podemos usar el amor para justificar el amor y ni siquiera la lógica para justificar la lógica.
Pues bien, Gödel, en sus destellos de genialidad que sólo la locura puede provocar, se dedicó a intentar comprender esto. Como el hambre y el amor son conceptos muy abstractos, intentó ceñirse a aquello con lo que a cualquier animal, incluso un humano, le resultaría fácil trabajar. Se apegó a los números. Y para no perderse en ellos decidió coger el grupo de números más común y aburrido, los números enteros (recordemos que los números enteros son todos los números naturales incluyendo el cero y los números negativos, (…, -2, -1, 0, 1, 2,...). Entonces pensó que cualquier sistema axiomático –es decir, cualquier conjunto de axiomas que pueda usarse para derivar lógicamente cualquier teorema– que pueda crearse para incluir la aritmética de números enteros, es decir, un sistema A formado por hipótesis iniciales de las que se derivan enunciados que tienen que ver con posibles operaciones matemáticas que involucran al grupo de números enteros no puede ser a la vez completo y consistente.
Qué locura, ¿verdad?
Sí, literalmente loco, Gödel no fue a un asilo para broncearse. Técnicamente lo que dijo, en el lenguaje de gente cuerda, es que si un sistema tiene consistencia, es decir, es estable, no puede ser completo, y si es completo no puede ser consistente. Si hay un sistema autoconsistente, entonces habrá proposiciones que no pueden ser probadas ni negadas por ese mismo sistema (es incompleto) y si el sistema es completo, no puede validarse a sí mismo (sería inconsistente). Esto significa que no se puede utilizar el hambre para demostrarlo, que se necesitaría una computadora fuera del universo para comprender el universo, que la lengua no puede saborearse a sí misma y que nunca podremos demostrar que 2+2=4.
“¿Y por qué es esto interesante?” Te preguntas: "¿Por qué pierdo el tiempo en esto?"
Empecemos por lo básico. Cuando dije que no podemos probar que 2+2=4, no me refiero a que no puedas poner dos plátanos frente a ti junto a dos peras y contar que hay cuatro frutas. Como dijimos, incluso los monos hacen esto. Pero deja la fruta a un lado, toma lápiz y papel y piensa en el pasado. Cuando eras pequeño, a tus profesores les encantaba abusar de ti con las tablas de multiplicar. Tablas de suma, resta, división y multiplicación. Si hoy puedes responder rápidamente cuánto es 5×4 o 11+3, no es porque sepas calcular, sino porque lo memorizaste. Ten en cuenta que responder qué es 7×8 o 11.347+32 no es tan rápido, a pesar de ser tan fácil de calcular como los primeros. Este condicionamiento desde pequeño sirvió para colocar en tu cabeza algunas verdades absolutas, por lo que desde pequeño creías que 2+2 es igual a 4. ¿Pero es realmente así? Veamos, piensa en un ejemplo de la vida real en el que trabajas con números negativos. Cualquiera que haya tenido o tenga una tarjeta de crédito lo encuentra fácil. Piensa en una situación en la que trabajas con fracciones. Cualquiera que haya pedido una pizza para 2 o más personas le ha ido bien con esta también. Ahora piensa en una situación en la que tienes que lidiar con la multiplicación de fracciones negativas. ¿Dónde encaja esto en tu vida diaria? Llega un momento en el que las cosas sólo tienen sentido sobre el papel.
Entonces tienes una manera de demostrar que 2 + 2 = 4. Tienes las matemáticas para eso. De la misma manera se puede demostrar matemáticamente que esto se puede demostrar matemáticamente. No sólo eso, sino que podemos demostrar que es posible demostrar que 2 + 2 = 4. Y esto también se puede demostrar.
Ahora 2 + 2 no es 23. Y podemos probar matemáticamente que 2 + 2 no es 23. Y podemos probar que podemos probar que 2 + 2 no es 23. Y podemos probar que podemos probar que podemos probar que . Y esto también se puede demostrar.
Entonces se puede demostrar que 2 + 2 no es 23. ¿Pero podría también demostrarse que 2 + 2 es 23? Parece una pregunta estúpida, pero es crucial. Si esto pudiera demostrarse, ¿dónde se esconderían avergonzados nuestros profesores de matemáticas? Sería devastador, porque si es posible demostrar que 2 + 2 = 23, entonces sería posible demostrar que 23 no es 23, como también podemos demostrar que 2 + 2 no es 23. Esto significaría que no No hay nada que no pueda demostrarse, y esto es sólo otra forma de decir que nada es cierto y por tanto todo está permitido y entonces todas nuestras certezas serían meras apuestas más o menos convenientes.
¿Estás confundido? Entonces escribiré más lento para que puedas intentar seguirlo.
Llegados a este punto debemos preguntarnos: ¿Existe alguna forma de demostrar que no se puede demostrar que 2 + 2 = 23?
Por supuesto, es posible que ya te hayas imaginado la impactante respuesta de Gödel. No sólo no podemos, sino que nunca lo haremos. Además: si se puede demostrar que nunca demostraremos que 2 + 2 = 23, ¿qué base tenemos para afirmar algo lógicamente? Y si no se puede demostrar ningún argumento como “demostrar que X no se puede probar”, entonces sabemos que la lógica y las matemáticas son tan inconsistentes como cualquier otra forma de creencia.
Gödel nos demostró que no podemos entender el universo si somos parte del universo, que no podemos entender el batido que estamos haciendo si estamos atrapados dentro de la licuadora. Para ello sería necesario que una mente o un ordenador ajeno a nuestro universo nos analizara. Y te pareció gracioso que hablar del 42 y la pregunta correcta no pudieran coexistir en la misma realidad, tsk, tsk...
Ahora bien, todo esto sería una conversación de bar interesante si se detuviera ahí, pero recuerden el comienzo del texto: Gödel solía estar institucionalizado. En hospicios. Por lo tanto, todo esto sólo sirve para el siguiente paso lógico – si todavía crees en esa superstición que llamamos “lógica”.
Aunque no se puede probar que 2 + 2 = 23, podemos probar que no se puede probar que 2 + 2 = 23. Entonces podemos probar que 2 + 2 = 23. Es decir, si pudiera ser demostrado que no se puede demostrar que 2 + 2 = 23 entonces también se podría demostrar que 2 + 2 es 23!
Confuso, ¿verdad? Pero esto no es un problema con tu capacidad de comprender sino más bien un problema con nuestra comprensión. De hecho, lo que hizo el bueno de Kurt fue expresar matemáticamente la antigua paradoja de la autorreferencia atribuida históricamente a Epiménides. Epiménides era de Creta y decía que todos los cretenses son mentirosos. Esto es como leer un cartel que diga:
"Esta frase es falsa".
Llamemos a esta frase declaración G en honor a Göedel. Ahora pregúntese: ¿es verdadera la afirmación G? Si G es verdadero entonces tenemos un enunciado válido que es falso, pero si G es falso entonces su enunciado es verdadero. En otras palabras, si la oración es verdadera es mentira, si es mentira entonces es verdadera. Es lo mismo que pedirle a Pinocho que diga la frase: “¡Ahora me crecerá la nariz!” ¿Qué piensas tú que sucederá?
Esto no significa que debamos abandonar la lógica y andar poniendo Amendocrem en los genitales de los niños, pero sí significa que G está incompleto. Lo mismo se puede hacer con cualquier otro sistema, demostrando que no sólo habrá errores que nunca podrán probarse como errores, sino que también habrá verdades que no podrán probarse. Y eso no es sólo en matemáticas. Piensa en Dios, en el amor, en la creencia de que el chocolate es bueno y el hígado es malo, que lo que crees que es correcto es realmente correcto. Estas son cosas que nunca se pueden probar ni descartar, no de una manera que podamos entender.
BONO
¿Aún no entiendes de qué estamos hablando? ¡Por los muslos de María! Seamos explícitos entonces. ¿Tienes ese lápiz y papel en tus manos?
1- Empecemos suponiendo que A y B tienen el mismo valor. Entonces A es igual a B.
2- Multipliquemos ambos lados por A.
3- Restemos ahora ambos lados de la ecuación por B elevado a 2.
4- ¿Recuerdas las matemáticas de la secundaria? Factoricemos ambos lados, es decir, veamos qué tienen en común y separemos, en este caso ambos lados tienen (AB) en común, así que factoricemos así.
5- Como tenemos (AB) multiplicando a ambos lados de la igualdad podemos dividir ambos lados por (AB) obteniendo este resultado.
6- Como dijimos al principio que A=B entonces A+B=B es lo mismo que B+B=B o A+A=A, nos quedaremos con la primera opción. Simplificando tenemos que B+B es igual a B por 2.
7- Ahora dividimos ambos lados por B.
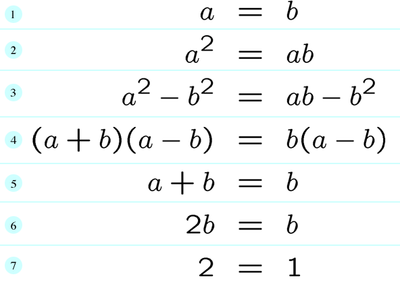

por LöN Plo