Este texto foi lambido por 702 almas esse mês
“É impossível deixar cair um alfinete sem causar uma reação correspondente em toda Estrela. A ação perturbou o equilíbrio do Universo.”
– Aleister Crowley, O Livro de Thoth.
A eloquência da compreensão de Crowley do que a ciência agora de “Efeito Borboleta” é evidente na citação acima. Esse nome estranho vem de uma colocação mais estranha ainda: “O bater de asas de uma borboleta em Tóquio pode provocar um furacão em Nova Iorque.” Esta frase não veio de nenhum monge budista ou mistico rosa-cruz, mas de um matemático do século XX chamado Edward Lorenz, pioneiro no estudo da Teoria do Caos e suas consequências.
A Teoria do Caos concebe um universo onde cada ponto é interligado, relacionado em um grande ‘Atrator Estranho/Repulsor’ e onde, portanto, todo evento está ligado a todos os demais e qualquer acontecimento acaba por alterar o destino de eventos localizados a milênios de anos-luz de distância. A Teoria do Caos considera a lógica clássica causa-consequência como algo simplista e até ingênuo e, em vez disso, trabalha com múltiplas causas e múltiplas consequências operando dentro de sistemas dinâmicos complexos. E por mais não-intuitivo que seja este é provavelmente o caso do universo em que vivemos.
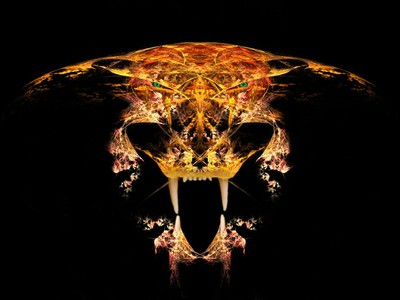
Em termos geométricos a teoria do caos se traduz nos chamados Fractais, figuras teoricamente infinitas e independente de escala, que fariam Euclides cortar os próprios punhos. Um fractal como o da figura abaixo, pode ser dividido em partes e cada uma delas guarda semelhança ao objeto original, e cada uma delas guarda informações com as quais todo conjunto poderia ser construído novamente.

Embora existam óbvios percursores, tanto a teoria do caos como os fractais são frutos da matemática da segunda metade do século XX. É muito curioso notar portanto que alguns anos antes estes conceitos já estavam presentes na ficção e em especial nas obras do famoso “Círculo de Lovecraft”, o movimento literário de amigos e fãs de H.P. Lovecraft que buscaram dar continuidade a sua obra.
Embora a matemática caótica seja usada para tentar se compreender o mundo em que vivemos, Lovecraft e o outros a utilizaram como uma porta para a consciência. Os magos do Caos logo notaram que os contos produzidos não eram simplesmente repletos de alegorias estéticas mas de chaves ocultas, de mapas da consciência que se dobravam e desdobravam sobre si mesmos. De passagens reais não para outros estados de consciência, mas para outras dimensões. E eles fizeram isso décadas antes que Mandelbrot, Lorenz & cia tirassem seus diplomas de conclusão do segundo grau.
Podemos ver retratos desta geometrização bizarra do universo na obra de ficção “A Droga Plutoniana” de Clark Ashton Smith. Segundo o Dr. Manners, o narrador da história, a droga cria “imagens plásticas incomuns, difíceis de serem traduzidas em termos de planos e ângulos euclidianos”. Esta incapacidade de ser processado em Matemática Euclidiana me traz à mente os fractais – no sentido de serem construtos não-euclidianos. Isso implica que eles não estão em conformidade com as formas geométricas geralmente aceitas, como triângulos, quadrados, etc. A droga também cria uma outra propriedade semelhante à encontrada em imagens fractais: ambos possuem “limites ou fronteiras” artificiais. A droga produzia “uma vasta distância que era totalmente desprovida de perspectivas normais, uma paisagem estranha e peculiar que se estendia indefinidamente, cruzada por um friso, ou baixo-relevo, ininterrupto de figuras humanas que corriam como uma imutável muralha reta.”
Além do fato de se referir ao friso como uma parede reta (um ponto que Smith expande para colocar ramificações ao longo da sua superfície), todas as outras descrições podem ser consideradas como sendo semelhantes às de muitas imagens fractais. Smith cria uma visão conde o tempo é como um fio de eventos – interligados, se alterando constantemente, produzindo um padrão abstrato. Este fio tem seu comprimento e complexidade infinitos, produzido em uma dimensão fractal que não pode ser acessada pela matemática euclidiana nem por um estado normal da mente. É interessante especular se o conceito científico de Espaço/Tempo poderia ser modelado em termos dimensionais fractais. Idéias recentes de universos sendo criados e bifurcados parecem sugerir que sim.
John Dewey Jones, em um texto enviado para a newsletter Amygdala, desenvolveu a idéia de fractais e da transcendência da mente em sua ficção sobre as Seitas Amygdalanas. (Nota: Amygdala é derivada da forma de amêndoa, ou seja, a forma do conjunto Mandlebrot, é também o nome de uma seção do cérebro que, de acordo com Mortimer Mishkin e Tim Appenzeller em seu artigo para a revista Scientific American de junho 1987, é, juntamente com o hipotálamo, a central de processamento e área geral de vínculo para as informações sensoriais, memória e desejo)
Jones escreve sobre “A Irmandade do Caminho Invisível dos Adeptos”, monges que visualizam o “objeto” (conjunto de Mandlebrot) como uma mandala, usando-o para a auto-transcendência e iluminação. Ele pinta um cenário de decadência, onde a antiga civilização entrou em colapso e a Irmandade têm que criar o objeto como uma imagem astral. Para citar o Abade da Irmandade: “Nós sabemos que os olhos podem perceber detalhes e gradações de cor mais sutis do que qualquer monitor pode exibir. Assim como os olhos são superiores e mais sutis do que o monitor, a mente é superior e mais sutil do que os olhos. E a alma é ainda mais excepcional e sutil do que a mente. Assim sendo, deixe o monge se retirar para um lugar tranquilo e expandindo seus sentidos, como os membros de uma tartaruga, deixe que fixe seus pensamentos firmes sobre o objeto. ”
A Irmandade reconhece dois caminhos que levam ao objeto: o primeiro através de sonhos, onde se obtemos de visões de “cores puras como jóias […] padrões de relações abstratas: alguns já afirmaram que seus sonhos foram extremamente claros e distintos para serem descritos em palavras”. Este é o tipo de descrição que me faz pensar na maneira como Lovecraft produziu algumas de suas melhores obras de ficção, acesso ao conhecimento através de sonhos. Conhecimento que de outra forma seriam inalcançáveis.
No entanto, Jones também escreve sobre o segundo método que leva ao objeto, como o abade explica: “… desperte às três da manhã e ir para o cume da montanha, sente-se .., e olhe fixamente na direção da Aldebaran – não acreditamos em qualquer conexão causal entre Aldebaran e o objeto, você compreende, mas descobrimos que a luz avermelhada da estrela estimula a visão matemática que buscamos”.
Já em “Os Sonhos na Casa da Bruxa”, o próprio Lovecraft, parece refletir o primeiro método da Irmandade nos sonhos do herói Walter Gilman. Lovecraft diz que “talvez Gilman não devesse ter estudado tanto. O cálculo não-euclidiano e a física quântica bastam para esgotar qualquer cérebro, e quando alguém os mistura com folclore, e tenta traçar um estranho pano de fundo de realidades multi-dimensionais, por trás das sugestões macabras das narrativas góticas e das desvairadas histórias sussurradas ao pé do fogo, dificilmente poderia evitar sofrer um grande stress mental”.
Gilman é impulsionado por seus interesses nos domínios da matemática abstrata “que iam além, talvez, às mais modernas pesquisas de Plank, Heisenberg, Einstein e Sitter”. Lovecraft descreve os sonhos de Gilman como “mergulhos através abismos ilimitados de crepúsculo de coloridos inexplicáveis e atordoantes sons desordenados; abismos cujas propriedades materiais e gravitacionais… ele não poderia nem começar a explicar.”
Ele continua … “Os abismos não eram de forma alguma desocupados, mas abarrotados com indescritíveis de massas angulares de substâncias que possúiam matizes alienígena, alguns dos quais pareciam ser orgânicos enquanto outros pareciam inorgânicos… Gilman às vezes comparava a matéria inorgânica a prismas, labirintos, aglomerados de cubos e planos… e as coisas orgânicas lhe pareceram várias vezes como grupos de bolhas, polvos, centopéias, ídolos hindus vivos, e arabescos intrincados inflamados em uma espécie de animação ofídica”.
Modelos Fractais dessas imagens podem ser descobertos em muitos dos livros sobre o assunto. Mandlebrot em “A Geometria Fractal da Natureza” descreve e mostra fotos de redes de apolônio, de conjuntos de Cantor e Fatou – quase-fractais parecidos com aglomerados de cubos e planos borbulhante. As curvas do floco de neve de Koch/Peano que se parecem com labirintos. Outros desenhos geométricos que são apresentados são o conjunto Mandlebrot, o conjunto de Julia, rabiscos (como o nome indica são figuras que parecem feitas de rabiscos) todos com semelhanças com os polvos, centopéias e arabescos intrincados. A forma chamada por Lovecraft de “ídolos hindus vivos” pode ser imaginada de duas maneiras, ou como o “formato” dos trabalhos fractais de Michael Barnsley, que você pode ver em seu livro “Fractals Everywhere” – Fractais Por Toda a Parte -, ou como biomorfos, sigilos caóticos gerados com fractais que se evoluem como organismo vivos, podendo assumir formas variadas.
No final da história Lovecraft descreve Azathoth como o caos final – semelhante a um conjunto Mandlebrot lapidado adornando uma coroa que dá forma à realidade.
Outras histórias de Lovecraft também aludem às imagens bizarras da Geometria Fractal. Os exemplos são: “Nas Montanhas da Loucura” onde ele usa geometria abstrata para descrever não apenas o labirinto formado pela antiga cidade dos Mais Antigos como também a auto-similaridade de seus corpos; “Através os Portões da Chave Prata”, onde os padrões abstratos observados por Randolph Carter no limiar do portal, são uma reminiscência de fractais fluidos eternamente se bifurcando. Uso de imagens fractais por Lovecraft no “Através os Portões da Chave Prata”, nos lembra a Droga Plutoniana, uma vez que ambos estão descrevendo viagens através do Espaço/Tempo de forma geométrica. Um exemplo disso é Randolf Carter, o herói da história de Lovecraft, ao fazer uso da Chave de Prata, se encontra cercado por “quase imagens sombrias, com contornos incertos em meio ao caos fervilhante, mas Carter sabia que eles eram memórias e imaginação. Mesmo assim, ele sentiu que não era o acaso o responsável pela construção dessas coisas em sua consciência, mas sim uma realidade vasta, inefável e adimensional, que o rodeava e era capaz de se traduzir utilizando-se dos únicos símbolos que ele era capaz de compreender”.
“O Case Pikestaffe”, de Algernon Blackwood, usa a geometria abstrata para habilitar que ‘Pikestaffe’ realize um viagem para uma dimensão extra, como “Alice através do espelho”.
A Lousa de Pikestaffe estava coberta de diagramas que “talvez fossem euclidianos, ou possivelmente astronômicos”. Ele também tinha anotações que possuíam equivalentes fractais, por exemplo, a senhoria de Pikestaffe descobriu notas com um diagrama que ela descreveu assim: “No centro, cercado por rabiscos hieróglifos, números, curvas e linhas sem sentido para ela, ela viu um diagrama do espelho completo”.
Por fim, Frank Belknap Long, em seu “Os Cães de Tíndalos”, usa conceitos semelhantes aos de Smith e Lovecraft, combinando os conceitos semelhantes aos da Droga Plutoniana e do Portal da Chave de Prata, para que seu personagem principal Halpin Chalmers viajasse de volta no tempo através do abismo final da geometria caótica. As “alegorias” Lovecraftianas acabaram definindo o nosso universo mesmo antes da ciência formal se aperceber disso.
por LöN Plo
Alimente sua alma com mais:

Conheça as vantagens de assinar a Morte Súbita inc.