Este texto foi lambido por 433 almas esse mês
Não vos percais com os preceitos da Ordem
– O LIVRO DO ÚTERO 1:5
NO PRINCÍPIO
Olhe para o céu em um dia ensolarado, sem núvens e diga o que vê. Se conseguir descrever algo é porque está olhando para o lugar errado. Procure no céu algo que perturbe o olhar, é uma forma esférica e luminosa, quando a encontrar, olhe diretamente para ela e diga o que vê. É o Caos. A Maçã da Discórdia em sua forma mais pura. É o sorriso da Deusa. Os macacos chamam esse Glorioso Explendor simplesmente de sol, ou ainda estrela, ou ainda astro, numa tentativa cada vez maior de enterrar Sua Sorriso Esquisofrenicamente Belo. Mas para poder compreender os macacos, temos que falar sua língua, e assim nós começamos nosso mergulho.
Macacos, perdão, cientistas, acreditam que o sol, e outras estrelas, mas vamos nos focar apens no sol, nada mais é do que uma bola gigante de gás. Mas não bastando acreditar nisso eles foram além, eles acreditam que os gases que formam essa bola ficam no lugar por causa do próprio peso. De cara já percebemos que existem duas palavras que não se encaixam em um descritivo de uma dama: bola e peso. Mesmo assim, continuemos.
Cada parcela do sol é atraída para todas as parcelas restantes pela força da gravidade[1], se precisar de uma imagem para conseguir entender isso, pense na atmosfera da terra sendo atraída para a terra. Agora, se temos uma quantidade discretamente chamativa, de gases sendo forçados em direção a um único ponto, o lógico seria que o sol fosse do tamanho da cabeça de um alfinete, certo? Isso poderia ser o caso, caso não fosse por outra força.
Imagine que está em um show. Imagine que é um show do AC/DC e você quer chegar perto da banda para vê-los tocar. Você tem duas opções:
A) Chega cedinho, assim que abrem os portões corre para a grade perto do palco, abraça a grade e espera.
B) Chega minutos antes da banda entrar, com o estádio lotado e força caminho rumo a grade.
Estou falando por experiência própria. Num show cheguei cedo e fui para a grade. A Banda entrou. Em dois minutos estava sendo pisoteado e meu braço estava sendo quebrado. Foi um show do cacete. No outro cheguei logo antes da banda entrar, forçando passagem consegui assistir a tudo a menos de 3 metros de distância do palco. Qual a licão que tirei dessas duas experiências?
No jogo da vida é melhor ser o gás sendo levado rumo ao centro do sol do que o gás que está no centro e não tem por onde sair.
Para o sol não desmontar sobre si mesmo a pressão em seu interior cresce de acordo com a força pela qual os gases são atraídos para o centro. Isso faz com que no centro a temperatura seja mais alta, a pressão maior, o número de coisas ocorrendo ao mesmo tempo loucamente incalculável. Faz com que quem está fora queira entrar e quem está dentro comece a desejar não estar naquele miolo. O sol de fato é muito semelhante a um show do AC/DC. Todo astrofísico deveria realizar este experimento para se aproximar daquilo que estuda de longe.
Aumente a pressão de algo, a temperatura aumenta, e qualquer pessoa que já esqueceu uma panela de pressão no fogão ligado conhece um dos fatos básicos da vida: você pode estar cercado de alumínio, pode estar cercado por ferro, pode estar cercado por uma liga metálica criada pela NASA, quando o calor resolve sair, ele sai. Assim essa energia que existe dentro do sol de pressão empurrando pra fora, gravidade puxando para dentro resulta, num primeiro momento em luz e calor. Mas num segundo momento resulta em muito mais.
Para resumir uma longa e chata história esse ciclo é cíclico, muito gás, muito peso, muita pressão no núcleo, essa pressão empurra tudo para fora, onde o peso faz voltar para o núcleo, etc… Mas afirmarmos que o sol é feito de gás é um erro, e como já demos várias explicações científicas desde o começo do texto vamos corrigí-la. O calor dentro do sol é tão descomunal e a pressão tão fodasticamente forte que, como no show do AC/DC, qualquer coisa lá no meio não tem forma. Se não possui uma forma básica que seja composta de alguma coisa menor não podemos nem dizer que aquilo é um gás. Por isso usam o nome plasma ou, trocando em miudos, aquilo que quando for deixado em paz vai virar a base para se formar átomos. O centro do sol é uma enorme sopa de energia nem em estado líquido, nem gasoso, nem sólido. Quando se afastam do centro essas partículas começam a se formar e do meio do Caos surge a primeira forma, poderíamos chamar de a primeira informação. Só que essas partículas estão alucinadas, como se tivessem passado o dia numa fissura atrás de crack e tivesse acabado de cheirar meio quilo de cocaína cada uma. Isso faz com que essas partículas recém formadas já saiam para bater cabeça umas com as outras, novamente, como no show. Quando partículas sub atômicas batem uma de frente com a outra numa velocidade grande o bastante o que acontece?
Bem, poderíamos dizer agora que Chernobyll foi não um acidente, mas uma homenagem à Deusa.
O núcleo do sol é como um reator nuclear boiando no espaço. Mas nem tudo é simplesmente bate cabeça. Quanto mais distantes do núcleo, mas as formas aparecem. Eventualmente várias partículas fogem do núcleo do sol, vários prótons e neutrons e elétrons, assim que a força do núcleo diminui um pouco sobre eles, graças à distância as forças nucleares fortes e fracas e o eletromagnetismo entra em ação e voilá, um elétrom fica preso na órbita de um prótom e ai você tem seu primeiro átomo da tabela periódica, o Sr. Hidrogênio. Quando eventulamente as estrelas entram em colapso, suas áreas cheias de hidrogênio são esmagadas em cima de si mesmas, o sol explode e nisso começa a fabricar hélio, que tem dois prótons e dois elétrons, e a coisa continua, cada vez que uma estrela entra em colapso ela começa a fazer os átomos que a constituem se fundir em átomos mais pesados, chegando no urânio que é a baleia dos átomos e serve pra fazer bombas. Eventualmente esses átomos são cuspidos para longe das estrelas quando elas explodem e vão para o universo, onde sob certas condições começam a se combinar em moléculas, e as moléculas se combinam em coisas maiores e logo logo surgem gases, líquidos e minérios. Por isso, sim! A culpa de você estar sem ter o que fazer na frente do computador é do sol – isso do ponto de vista do macaco. Do ponto de vista correto isso significa que todos viemos d’Ela, cada micro parte de nosso ser, vomitado por suas maçãs espalhadas pelos cosmos.
Esse processo explica como um bando de matéria solta se une, forma uma estrela e começa a cuspir átomos que viram outras coisas como gasosas, planetas e você ou eu. Acredita-se que no início do universo havia apenas hidrogênio e hélio, por um lado esses dois elementos partiram de uma sopa violenta de energia, que só existia por causa do Caos e por outro esses dois elementos, depois de milhões e milhões de anos de abuso, foram transformados em outros elementos. Como a Deusa sorri para sua criação de todos os ângulos que podemos perceber não é surpresa descobrir que isso vem acontecendo pelos últimos 17 bilhões de anos.
Se chegou até aqui ótimo, você acabou de me ver explicando dois processos interessantes:
1- Fusão Nuclear
2- Matemática
APÓS O PRINCÍPIO

Resolvi sair na rua e brincar um pouco. Escolhi a rua porque ela fica mais longe da wikipedia do que a casa e locais de trabalho dos outros. Também escolhi a rua porque vivemos em uma sociedade onde as pessoas tendem a despirocar quando aparece dentro de suas casas e locais de trabalho uma pessoa estranha. E assim sai pelas calçadas com uma prancheta na mão, um crachá no bolso do paletó e meu melhor sorriso de vendedor de carros usados perguntando para as pessoas coisas como nome, número do rg, endereço, idade, telefone, grau de escolaridade e o que é matemática. Descobria algumas coisas interessantes com isso.
Primeiramente descobri que mesmo vivendo em uma sociedade onde as pessoas despirocam quando aparece dentro de suas casas e locais de trabalho uma pessoa estranha, elas não tem problemas para dar seus dados para uma pessoa estranha se ela está segurando uma prancheta e sorrindo para elas.
Segundamente descobri que quanto mais velhas e supostamente instruidas, mais estúpidas ficam as pessoas. Vejam, as pessoas mais velhas e com maior grau de instrução respondiam que a matemática é O ESTUDO DOS NÚMEROS. As mais jovens e com menos instrução respondiam que a matemática é A CIÊNCIA DOS NÚMEROS. As crianças de até 7 anos que responderam a pesquisa afirmaram que NÃO SEI O QUE É MATEMÁTICA, mesmo quando o responsável presente insistia em querer contaminar a jovem mente com a idiotice da maturidade.
Ponto para as crianças. Não há como explicar o que é a matemática.
Cientistas são por definição pessoas preguiçosas. Sempre que vão fazer estudos com animais perdem anos ensinando a eles como se comunicar de forma humana para tentar entender o que os bichos pensam ao invés de simplesmente aprender a línguagem dos bichos e experienciar o que eles pensam. Tente ler Finnegan’s Wake do Joyce em qualquer tentativa de tradução e logo vai entender o problema com essa preguiça científica.
Para evitar cair no mesmo erro eu dediquei horas e dias aprendendo a linguagem dos macacos e transcrevo aqui exatamente o que eles pensam sem traduções grosseiras.
O Dogma Simiesco afirma que:
“É fato sabido que a espécie humana já conhece os números abstratos há cerca de 8.000 anos. A matemática formal, simbólicam com equações, teoremas e provas, tem pouco mais de 2.500 anos. O cálculo infinitesimal foi desenvolvido no século 17; os números negativos passaram a ser usados comumente no século 18, e a álgebra abstrata moderna, onde símbolos como x,y e z denotam entidades arbitrárias, tem apenas 150 anos.”
O macaco que disse isso não é um macaco qualquer, ele é Keith Devlin, um macaco que atingiu o cargo de diretor executivo do Centro de Estudos de Linguagem e Informação, além de professor do Departamento de Matemática da Universidade de Stanford, assim como pesquisador da Universidade de Pittsburgh, nas horas vagas ele é membro da American Association for the Advencement of Science. Como eu disse, parece qu equanto mais velha e instruída, mais estúpidas ficam as pessoas.
Nosso amigo prossegue com uma rápida linha do tempo da matemática que tenta explicar do que ela se trata:
– Até 500 a.C. a matemática era algo que tratava de números. A matemática do antigo Egito, Babilônia e China consistia quase que inteiramente em aritmética. Era largamente utilitária e de uma variedade bem do tipo “livro de receitas” (Faça isso e aquilo com um número e você terá a resposta).
– Entre 500 a.C. e 300 d.C. a matemática se expandiu além do estudo dos números. Os matemáticos da antiga ©récia se preocupavam mais com a geometria. Na verdade eles viam os números de uma perspectiva geométrica, como medidas de comprimento, e quando descobriram que havia comprimentos aos quais não correspondiam seus números (chamados comprimentos irracionais), o estudo do assunto praticamente estancou. Para os gregos, com sua ênfase em geometria, a matemática era números e forma. Foi somente com os gregos que a mamtemática realmente passou de um conjunto de técnicas para se medir, contar e calcular para uma disciplina acadêmica, que tinha tanto elementos estéticos quanto religiosos.
– Depois dos gregos, embora a matemática progredisse em diversas partes do mundo – notavelmente na Arábia e na China -, sua natureza não mudou até meados do século 17, quando sir Isaac Newton (na Inglaterra) e Gottfried Leibniz (na Alemanha) inventaram, independentemente, o cálculo infinitesimal. O cálculo infinitesimal, em essência, é o estudo do movimento e da mudança. A matemática tornou-se o estudo dos números, da forma, do movimento, da mudança e do espaço.
 – A partir de 1750 houve um interesse crescente na teoria matemática, não apenas em suas aplicaçnoes, à medida que os matemáticos procuravam compreender o que estava por trás do enorme poder do cálculo infinitesimal. Ao final do século 19, a matemática havia se transformado no estudo dos números, forma, movimento, mudança, espaço e das ferramentas matemáticas que são usadas nesse estudo. Este foi o início da matemática moderna.
– A partir de 1750 houve um interesse crescente na teoria matemática, não apenas em suas aplicaçnoes, à medida que os matemáticos procuravam compreender o que estava por trás do enorme poder do cálculo infinitesimal. Ao final do século 19, a matemática havia se transformado no estudo dos números, forma, movimento, mudança, espaço e das ferramentas matemáticas que são usadas nesse estudo. Este foi o início da matemática moderna.
Bem, vocês sentiram esse cheiro? Parece comida digerida, descolorada e largada ao vento? Aquele cheiro fresco de merda?
SIM!!! É chegado o momento do selo.
 Como qualquer um pode ver, toda essa exposição é uma grande pilha de merda. Mas não há motivos para nos chatearmos. Qualquer jardineiro sabe que é na merda que crescem as flores.
Como qualquer um pode ver, toda essa exposição é uma grande pilha de merda. Mas não há motivos para nos chatearmos. Qualquer jardineiro sabe que é na merda que crescem as flores.
Vejamos que flores podemos colher dai.
1ª Flor
No post anterior vimos que números são coisas sinistras, vamos expandir aqui essa noção baseadas em fatos. Números são invenção de nossas mentes, a matemática, como veremos, não precisa em absoluto de números para ser conduzida.
2ª Flor
Não houve um período em que a matemática adquiriu elementos religiosos, ela teve sua origem na religião, como veremos.
3ª Flor
Essa evolução da matemática parte de um ponto de vista técnico e não natural. Veja porque agora.
Muitos construtores, fossem arquitetos, engenheiros, agrimensores, artesãos, perceberam que para se fazer qualquer coisa é preciso se trabalhar com proporções. Para se erguer uma coluna de tantos metros precisamos de pedras de tal tamanho. Para se fazer uma ponte assim e assado, precisamos de tanta madeira e tanta corda. Para se construir pássaros metálicos autômatos que cantam sozinhos, precisamos de tanta água e tanto metal, e as coisas precisam ser montadas de tal forma para que o sopro do ar imite o canto dos pássaros.
Logo eles descobriram que a matemática tinha uma forma de fazer essas proporções se tornarem perceptíveis e maleáveis, e passarma a usá-la como ferramenta de trabalho, da mesma forma que a Igreja Católica passou a usar Deus e Jesus e Maria como ferramentas de trabalho.
Assim não é de se espantar que quando Newton e Leibnitz começaram a brincar de cálculo que os cientistas da época resolvessem criar uma modinha de se usar matemática pra tudo. Como a física era o ramos da ciência que mais dava status, todos queriam ser físicos, e assim a matemática, coitada, ficou presa à física. Veja que na época quase tudo que era considerado matemática tinha a ver com a física. Depois disso ela evoluiu e tomou outros rumos, como matemática pura por exemplo, que descarta a necessidade de um mundo para a ciência existir.
Por isso, sempre que procuramos uma história da matemática, quase sempre encontramos uma descrição de seu desenvolvimento e evolução do ponto de vista que vai do primitivo e supersticioso, e também inteiramente prático até o século XVII e XVIII, e ai se torna uma arte física, e a partir dai o quanto ela se distancia da física. Assim temos uma noção primitiva e mística/supersticiosa de matemática, temos a criação da matemática moderna por homens brancos e religiosos e depois temos a evolução da matemática nas mãos desses homens brancos e religiosos que agora gostam de se intitular de Ateus para poder dizer que eles inventam a matemática, e não algum Deus de barbas brancas.
Bom, em um ponto esses homens brancos acertaram, a matemática não veio de um Deus de barbas brancas, veio de uma Deusa com sérios problemas bipolares – como toda deusa que se preze tem que ter.
4ª Flor
E talvez a mais importante. Por mais cavalhereisco que você seja, nunca foda com um alemão que inventa uma forma nova de se usar a matemática. Ele com certeza vai descobrir onde sua mãe mora. A fama nem sempre vale o preço que estamos dispostos a pagar.
Amarrando nosso lindo buquê
Temos então a visão clara de que grande parte do estudo matemático e da história da matemática é racista e chauvinista. Mas não se preocupe, vamos começar a corrigir isso agora.

Já vimos que um dos efeitos colaterais de nosso sistema nervoso, isso para não dizer da vida, é a capacidade de reconhecer pequenos grupos e notar pequenas diferenças de mudanças nesses grupos. Essa capacidade é aquilo que evoluindo se torna a capacidade de contar. Essa capacidade de reconhecer grupos e mudanças é facilmente confundida não apenas com contagem como com uma persepção ou senso de números. Vejamos alguns experimentos interessantes realizados com bebês e pessoas acidentadas.
Em 1967 Jacques Mehler e Tom Bever decidiram brincar com crianças. Não de uma forma suja e bizarra, mas cientificamente. Até então muitas pessoas não sabiam se bebês podiam contar ou tinham uma mínima noção de grandezas. Até então não havia testes que pudessem dar respostas claras do que os bebês achavam ou pensavam. Até os dois supracitados cientistas perceberem algo.
Eles reuniram crianças entre dois e quatro anos, e apresentaram para elas dois grupos de doces. Ao invés de testes onde haveria qualquer necessidade de comunicação a coisa foi resolvida da seguinte maneira. Na frente de cada criança colocavam dois grupos de doces, um com seis M&Ms, agrupados juntos e outro com quatro M&Ms espaçados. A idéia era criar um grupo de aparência menor, com mais docês e um que ocupasse mais espaço e tivesse menos doces. Então diziam para as crianças escolherem qual grupo de doces queriam. A grande maioria das crianças não pensava duas vezes antes de atacar o grupo mais compacto porém com mais doces.
Em 1980 resolveram ir além e testar crianças ainda mais novas. Prentice Starkey, na Universidade da Pensilvânia, fez um teste com 72 bebês com idades variando entre 16 e 30 semanas de vida. Ela colocou os bebês no colo da mãe e ambos na frente de um monitor. Sem avisar o bebê, como se ele estivesse em uma pegadinha do Mallandro, Prentice filmava os olhos dos bebês para poder cronometrar o tempo que ele investia observando algo. A lógica é muito boa, simples e muito MUITO boa. Se um bebê encara algo por muito tempo está prestando atenção – da forma que bebês prestam atenção – se os olhos ficam vagando de um lado para outro é porque perderam o interesse.
Nas telas exibiam slides, sempre que os olhos do bebê perdiam o interesse um novo slide era mostrado. E o que era mostrado era o seguinte: uma tela com dois pontos dispostos mais ou menos horizontalmente. Assim que o olhar mudava de direção surgia um novo slide com dois pontos em direções diferentes. Ela notou que a cada novo slide o tempo de atenção era menor. De repente, sem aviso, mostravam três pontos. Imediatamente o bebê voltava a se interessar, encarando o monitor por um período grande de tempo de 1.9 segundos, subia para 2.5 segundos.
A mesma experiência era feita ao contrário. Três pontos em posições aleatórias eram mostrados, sendo detectada uma crescente falta de interesse. Assim que era substituído por dois pontos o interesse voltava.
Algum tempo depois foram feitos experimentos que comprovaram que bebês com 2 ou 3 dias de vida conseguiam descriminar mudanças em no tamanho de conjuntos.
Essas e inúmeras outras experiências do tipo provaram que bebês conseguem lidar com mudanças em conjuntos que contenham 1, 2 ou 3 objetos. As crianças com menos de um ano parecem não saber distinguir 4 objetos de qualquer número maior. Mas o interessante é que essa habilidade não é exclusividade de crianças e bebês, em experimentos onde adultos tem que responder quantos pontos, arranjados de maneira aleatória, aparecem em uma tela, o tempo necessário para darem a resposta quando surgem um ou dois pontos é praticamente idêntico, para reconhecer três pontos levam pouco mais de meio segundo, mas quando o número de pontos ultrapassa o três o tempo de reconhecimento começa a subir, e conforme o número de pontos cresce o número de erros cresce também. Isso deixa claro que as respostas são resultados de dois processos cerebrais completamente diferentes. Até três nós reconhecemos imediatamente a quantidade, além de três nós contamos quantos objectos estão presentes. Quando o número de pontos nos slides aumenta, o tempo requerido para que a cobaia cuspa o resultado também aumenta. Linearmente. Ou seja, demora mais porque está contando, e números maiores precisam de mais tempo para serem contados. Duvida? Conte até 10 mentalmente. Que número chega antes? o 7 ou o 3?
1, 2 e 3 são “valores”, “quantidades”, “padrões” que reconhecemos instintivamente. Sem pensar. Da mesma forma que a vespa talvez não fique imaginando que precisa arranjar a raiz quadrado de 25 lagartas para deixar com seus ovos. Isso me faz crer que 1, 2 e 3 não sejam números de fato. Numeração começa além do quatro. Se preferir podemos inverter e eu afirmo que os únicos números que existem em nosso cérebro são o 1, o 2 e o 3, e a partir do 4 são outra coisa qualquer. Desenvolverei essa ideia com o tempo.
Bem, além de preguiçosos, cientistas e homens da razão em geral tem uma diversão depravada curiosa: adoram passar décadas reinventando a roda.
Releia os experimentos antes de prosseguir. Para facilitar a compreensão vamos seguir certa ordem cronológica.
1- A moda hoje é afirmar que o Antigo Testamento foi escrito na época do rei Salomão, que afirmam ter sido por volta de 1009a.C. a 922 a.C. No livro Gênesis 1:26-27 (negritos meus)
E disse Deus: Façamos o homem à nossa imagem, conforme a nossa semelhança; e domine sobre os peixes do mar, e sobre as aves dos céus, e sobre o gado, e sobre toda a terra, e sobre todo o réptil que se move sobre a terra.
E criou Deus o homem à sua imagem: à imagem de Deus o criou; homem e mulher os criou.
E Deus os abençoou, e Deus lhes disse: Frutificai e multiplicai-vos, e enchei a terra, e sujeitai-a; e dominai sobre os peixes do mar e sobre as aves dos céus, e sobre todo o animal que se move sobre a terra.
2- Lao-tsé, em seu Tao-te king, escreveu, na China, no ano 500 a.C:
“Tau a Razão criou Um. Este Um tornou-se Dois, e o Dois produziu o Três, e o Três produziu todos os outros seres”.
3- Platão, que viveu entre os anos 427 a.C. e 348 a.C. (dando ou tirando um ou dois anos), escreveu:
“O ser humano foi criado no início com o homem e a mulher não formando mais do que um só corpo.
Cada corpo tinha quatro braços e quatro pernas. Os corpos eram redondos e rolavam por toda parte, servindo-se dos braços e pernas para se mover. Acabaram por desafiar os deuses. Um deus disse então: “Matemo-los, pois são muito perigosos‖! Um outro disse: “Não, tenho uma idéia melhor.
Vamos dividi-los em dois; assim não terão mais que dois braços e duas pernas; não serão mais redondos. Não poderão rolar; sendo dois oferecerão o dobro de sacrifícios e, o que é mais importante, cada metade estará tão ocupada procurando a outra que não terão tempo para nos desafiar”.
4- Manava Dharma Sastra, antigo livro hindu datado do século 1 a.C. traz o seguinte texto:
“No começo só existia o infinito, chamado aditi. No infinito se encontrava A U M, razão pela qual deve preceder toda prece ou invocação”.
O Livro de Manu, antiga obra hindu, diz: “A sigla A U M significa terra, céu e paraíso”.
5- Uma tábua de argila encontrada por William Niven no México datadas de ?! e batizada como tábua número 150, lemos uma lenda Nacal de como a terra foi povoada:
“O Criador criou Um, Um se tornou Dois”.
“Dois produziram três”.
“Destes três descende toda a humanidade”.
digo datadas de ?! porque alguns entusiastas do impossível chegam a datar as tábuas de mais de 12.000 anos atrás. Investigaremos isso a fundo e talvez coloquemos a data correta.
Ainda entre os Nacals existe o seguinte símbolo:

Ele é um dos três símbolos formando um parágrafo que significa:
O criador é Uno. Ele é dois em um, Lahun. Esses dois formam o Filho – o Homem Mehen.
Este gráfico é chamado também de “o texto misterioso”, porque de qualquer maneira em que seja lido, começando-se de qualquer ponto do triângulo formado pelos símbolos, o significado permanece o mesmo: um, dois,
três.
6- Em 1967 John Lennon compôs uma epifania musical, que se inicia com:
I am he as you are he as you are me and we are all together.
Para ilustrar melhor eu costumo dividir em:
|I am he| as |you are he| as |you are me| and |we are all| to get her!
Agora tentem notar alguma similaridade entre aquilo que foi descoberto com crianças e esses textos citados.
Alguém?
Nos diz muito a respeito de nosso cérebro como podemos pensar “que coincidência a religião e a filosofia tratarem de trindades e termos uma capacidade inata de distinguir grupos de três” mas não achamos coincidência que os isótopos de ferro que são cuspidos por super-novas como isótopos radioativos de níquel e cobalto nas proporções exatas que encontramos no ferro usado para fazer martelos aqui na terra.
Em um primeiro momento essa conexão pode parecer estranha. Mas vamos analisar outras coisas que não tem nada a ver com isso por hora.
Dê uma olhada com calma na figura abaixo. Me diga o que acha que ela é.
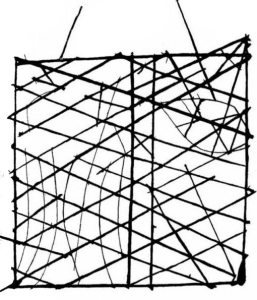
O engraçadinho que respondeu que isso se parece com o raio X da mochila de alguma senhora embarcando para o Paraguai terá a cabeça sodomizada mais tarde. Isso é um Mattang, um mapa. Ele é confeccionado com fibras de palmeira, gravetos ou qualquer coisa que possa ser usada para traçar linhas e curvas.
Para dar uma idéia do que exatamente é uma dessas coisas chamaremos Pablo.
PABLO! TRAGA O MATTANG!

Como podem ver, o Mattang de cima é uma versão do que Pablo, nosso Travesti de estimação segura. Espere.
PABLO! SUA BESTA, VIRE ELE!

Pronto, agora dá pra reconhecer aquele padrão de folha na parte superior direita, as duas retas paralelas no centro e as linhas curvas na esquerda em baixo.
Falemos sobre mattangs agora.
Os ilhéus do pacífico costumavam navegar bastante de uma ilha para outra. Vai ver eles se enchiam das pessoas presas com eles na própria ilha, vai ver eles ouviam sobre festas nas ilhas visinhas. Algumas das ilhas eram próximas umas das outras, algumas estavam distantes centenas de quilómetros. Esses ilhéus eram o que você provavelmente chamaria hoje de “índios”, ou seja, suas viagens eram realizadas em pequenos barcos e sem a ajuda de qualquer instrumentos de navegação moderno. Por serem “índios” eles não dispunham de bússolas, sextantes, ou mesmo de cartas de navegação. Latitude e longitude deveriam soar como marcas concorrentes de refrigerante para eles. Mesmo assim, eles pegavam seus barquinhos de “índio” e se metiam no mar para ir atrás das outras ilhas. E acredite, eles chegavam onde queriam.
Na falta de civilização para os entreter, esses ilhéus se ocupavam com outras coisas que estavam por perto, como por exemplo o mar. Na verdade o mar não estava apenas por perto, ele estava em volta, se estendia até o infinito e em algumas épocas também estava por cima. Com o tempo esses ilhéus aprenderam a reconhecer o padrão formado pelas ondas. Não apenas as que rebentavam em suas praias, mas as ondas no meio do caminho. Pelo movimento das águas na superfície do mar, mesmo que não houvesse qualquer vestígio de terra à vista, eles sabiam exatamente onde estavam por saber que desenho as ondas se formavam lá.
Como eles dependiam da navegação para muitas coisas, eles tinham “escolas de índios” que ensinavam os jovens a reconhecer esses padrões. Um dos “livros didáticos de índios” que eles usavam eram os mattangs. No mattang eles colocavam a posição de onde estavam, dos desenhos das ondas ao redor, no meio e no final dos vários percursos. Também contavam com a ajuda do sol e das constelações, além de pássaros, mas o mattang era o simulador de vôo que eles dispunham.
Agora pense no seguinte. Se o mar fosse sempre o mesmo, nós seríamos estúpidos de não nos guiar por seus padrões, mas ele não é o mesmo. Para começar ele é feito de água, e água, diferente de concreto, costuma ter uma natureza muito mais maleável e insconstante. Além disso se venta um dia num canto, ou tem um tsunami do outro lado do mundo, as ondas são afetadas e mudam de forma certo? Como conseguir se guiar por padrões que estão constantemente sujeitos a mudanças? Como gravar esses padrões em muttangs para que eles pudessem ser ensinados a jovens e crianças para que eles os reconhecessem quando os vissem? Se o mar muda o tempo todo, como um navegador índio da Oceania consegue saber onde está, a qualquer momento, apenas olhando para o mar?
Deixemos os índios de lado, vamos voltar para a civilização pelo momento. Claramente vocês se lembram de eu ter citado “pessoas acidentadas” mais acima. Vamos a elas.
Esta é Signora Gaddi. Ela sofreu um derrame. Mas males o menor e o derrame deixou sua faculdade de fala e de rascioncíneo, mas fudeu completamente com sua capacidade de reconhecer números. Ela literalmente não conseguia determinar ou avaliar o número de objetos em qualquer conjunto. Ela também só conseguia repetir os “nomes” dos números até o 4, e assim só conseguia contar os elementos de um grupo de quatro ou menos objetos.
Esta é Frau Huber. Ela teve que fazer uma operação. Enquanto a maioria das mulheres de hoje opera para tirar um pouco de gordura ou colocar muito silicone, Frau Huber queria retirar uma parte de seu lobo pariental esquerdo; não era exatamente vaidade, ela tinha um tumor lá. Depois da cirurgia, sua inteligência e capacidade de falar pareciam ter permanecido bastante boas, mas os números não. Ela também conseguiu foder sua capacidade de reconhecer números. Ela não conseguia somar nem multiplicar nem mesmo usando os dedos. Ela repetia a tabuada de multiplicação, mas era como se estivesse recitando um poema, nada daquilo fazia sentido. Ela continuava capaz de aprender que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa, mas apenas como você consegue decorar que a energia é a massa vezes a velocidade da luz ao quadrado. Não fazia sentido nenhum, se mostrasse um triIangulo retângulo de catetos igual a 3 e 4 e pedisse para dizer quanto media a hipotenusa ela repetiria a fórmula, mas não saberia calcular ou dizer ou entender aquilo.
Em Paris, algum tempo atrás, uma pessoa que vamos identificar aqui como “o paciente” sofreu um acidente. Sim, ele deve ter recebido flores. Sim, ele deve ter usado um daqueles aventais de hospital que deixa a bunda de fora. Não ele não morreu. Na verdade para deixar mais misterioso nem vou dizer se O Paciente é ele ou ela. Ao invés de morrer seu cérebro sofreu uma lesão que deixou o cérebro basicamente intacto, a não ser por sua capacidade de contar. Ele conseguiu foder sua capacidade de reconhecer números. Isso não significa que O Paciente não conseguia somar 2 mais 2. Isso significa que se você colocasse cinco objetos na frente d’Ele, Ele não saberia dizer quantos eram. Se colocasse dez objetos a mesma coisa. Curiosamente quando 3 pontos eram mostrados para ele em um slide ele conseguia repetir corretamente o número de pontos.
Claro que apenas usar acidentados para conseguir ibope pode parecer de mal gosto. Vamos ver pessoas que não precisaram foder sua capacidade de reconhecer números, elas já nasceram com a capacidade fodida.
Este é Charles. Ele é um jovem muito inteligente. Ele é graduado em psicologia. Ele precisa de uma calculadora para somar 2+2. Vejam, ele é de fato inteligente. Ele se graduou em psicologia e não em frentistologia, e ele não consegue somar 5+8. Isso não quer dizer que ele não consiga, ele usa a calculadora, lembra-se? Ele consegue usar a calculadora para fazer as contas e percebe o resultado, mas nada do que ele digita nela ou ela lhe mostra faz sentido algum. Quando a conta é simples e ele tem tempo ele usa os dedos, conhece os nomes dos números, mas não os enxerga. Dê dois números a ele como 20 e 2, ou 14 e 10.937.498 e pergunte qual o maior. Ele não saberá dizer, ele começa a contar nos dedos e vê qual chega primeiro, esse, logicamente, é o menor. Em um teste ele levou oito segundos para somar 8 e 6, em outro levou doze segundos para subtrair 2 de 6. Ele não conseguiu realizar contas mais complexas como 7+5 e 9+4. Obviamente ele levou mais tempo do que seus amigos para se formar, mas se formou.
Aquela ao lado de Charles é Julia. Não eles não tem qualquer parentesco, nem se conhecem. Como Charles, Julia também se graduou e não apenas isso, ela fez pós graduação. Como Charles ela também só conseguia contar usando os dedos e quando os números iam além do 10 ela suava frio e sentia os olhos se encherem de lágrimas, quando os dedos terminavam, também terminava a contagem. Frações para ela eram algo incompreensível, apesar dela ser capaz de cortar um bolo de aniversário em pedaços. Ela não consegue contar de 3 em 3, a não ser na mão, um a um e enfatizando cada terceiro nome: um, dois, TRÊS, quatro, cinco, SEIS, sete, oito, NOVE, etc., etc., ETC. Diferente de Charles, Julia conseguia dizer se um número era maior do que outro.
Que lições podemos tirar disso? Em primeiro lugar parece que um daltonismo para números é possível. Depois que chamamos pessoas que não percebem cores, pessoas que não percebem números, pessoas que não percebem dor de deficientes, mas pessoas que não percebem a Deus de Ateus, e por algum motivo esses “ateus” parecem se colocar em um grupo acima ao dos daltônicos, das pessoas com deficiência no senso numérico e das pessoas acometidas de Alopecia.
Há uma terceira lição que pode ser interessante. As pessoas lesionadas ou que não tem esse senso de número mostram que aquilo que chamamos de números parecem parasitar uma área específica do cérebro. Uma área diferente da parasitada pela linguagem. Dito isso podemos também afirmar que… ok, bando de covardes.
Dito isso eu afirmo que a matemática, assim como a linguagem, possuem circuitos próprios que já vem instalados em nosso sistema nervoso. Quando essas placas de circuito se quebram deixamos de contar ou de falar. Isso separa a matemática de nós, de cara. Nós somos equipados com o hardware, mas o software não vem de nós, nós apenas a descobrimos. E digo mais. Não precisamos de números para realizar matemática. E vou além! Aquilo que chamamos de números, não são o que você acha que são.
Caso você ainda pense que a matemática é inventada ou criada pela mente superior do homem moderno, pense nisso antes de dormir: se o teorema dos quadrados dos catetos não tivesse sido “inventado” antigamente para você calcular uma hipotenusa, ele eventualmente seria inventado em algum ponto da história, exatamente igual. O mesmo para teoremas e fórmulas mais complexas. Se um teorema ou fórmula não depende da mente superior de um “homem” específico para vir a existir como a compartilhamos? Se a matemática é uma invenção da mente, de quem é a mente que a cria?
eis sua MÃO!!!
Por LöN Plo
Alimente sua alma com mais:

Conheça as vantagens de assinar a Morte Súbita inc.