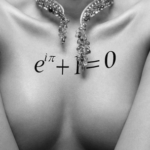Pi – Amor, Loucura e Formigas

Leia em 20 minutos.

Este texto foi lambido por 245 almas esse mês

Got to be a joker, He just do what he please

No início deste milênio – ou no final do milênio passado, depende se você é do tipo que conta ou mede o tempo – uma descoberta científica desconcertante, incrível, dessas que mudaram as bases daquilo que chamamos de realidade! Uma descoberta tão  SUPERFANTASTICABRITA que passou completamente desapercebida por você, por seus conhecidos, pelo fantástico e por mais de 99% da população do mundo (mais de 6.930.000.000 de pessoas se podemos acreditar na precisão dos informativos que vem impressos nas bandejas do Mac Donalds).

A descoberta foi realizada por Eamonn B. Mallon e Nigel R. Franks, do Centro de Matemática Biológica na inglaterra, e foi publicada no dia 22 de Abril no Proceedings of the Royal Society of London B.

Eamonn e Nigel estavam estudando um cordão da espécie Leptothorax albipennis e SIM!!! Este é um artigo sobre insetos que são mais fodas em matemática do que você – cordão é o coletivo de formigas.

Mas continue lendo.

As formigas Leptothorax albipennis habitam pequenas fendas nas rochas planas. Um cordão, ou colônia se preferir, consiste de uma única rainha, a sua ninhada, e de 50 a 100 trabalhadores. Quando um ninho é destruído, a colônia envia olheiros para avaliar possíveis novos locais de nidificação – puxa quantas palavras novas você está aprendendo hoje!

Se existem opções, há uma preferência por ninhos que possuam um determinado tamanho padrão – que está relacionado com o número de formigas da colônia. Isso só para começo de conversa já começa a ser meio assustador. Sabemos que animais tem certas “capacidades matemáticas” como contar e realizar operações, criar padrões fractais para optimizar caçadas, se utilizar de geometria para criar ninhos ou como forma de comunicação… mas calcular a área de uma toca?

Lembre-se que o ser humano padrão precisou perder o rabo, descer da árvore – não necessariamente nesta ordem – e desenvolver um super cérebro para poder começar a brincar de medir áreas. As formigas parecem ter achado que essa evolução toda era uma perda de tempo e resolveram usar aquilo que existe dentro de suas cabecinhas para fazer isso sem ter que esperar a invenção da calculadora para auxiliar.

Mas como elas fazem isso?

Mallon e Franks coletaram formigas de áreas próximas à costa de Dorset, na Inglaterra, e passou a criá-las em laboratório. Eles então transferiram as colionias para pratos de Petri quadrados grandes e ofereceram a elas várias opções de cavidades para formarem seus habitats; todas elas feitas a partir de pares de lâminas de microscópio com paredes de papelão preenchendo o espaço estreito entre o chão de vidro e teto de vidro.

“Usamos esses ninhos de lâmina de microscópio com cavidades de diferentes tamanhos, formas e configurações a fim de analisar as preferências”, afirmaram os desbravadores.

E o que eles perceberam?

Que experimentos que envolviam uma formigas marcadas individualmente mostraram que o olheiro – ou batedor se preferir um nome mais medieval – gastava em média 2 minutos correndo dentro de qualquer cavidade de forma aparentemente irrefletida e sem sentido. Outra coisa que perceberam é que o batedor acaba fazendo duas visitas a um local considerado aceitável para o futuro ninho, antes de recrutar seguidores.

E o que foi que eles notaram?

Que quando o batedor explora inicialmente um potencial ninho, ele cria uma trilha de ferormônio. Em sua segunda visita a sua corrida tresloucada na verdade serve para se criar uma pista diferente, uma que cruza várias vezes a trilha original.

Mallon e Franks então começaram a pensar que talvez o batedor consiga estimar a área do ninho em potencial detectando o número de intersecções entre o primeiro e o segundo conjunto de trilhas. A resposta se tornou clara!

As formigas não precisaram evoluir um cérebro para inventar calculadoras para medir áreas porque elas conseguem usar algoritmos para fazer isso. E você ai tentando se lembrar a diferença entre um algoritmo e um logaritmo! As formigas fariam isso de olhos fechado caso possuíssem pálpebras. Elas simplesmente sabem que uma área estimada, chamemos de A, de uma superfície plana é inversamente proporcional ao número de intersecções, chamemos de N, entre dois conjuntos de linhas, digamos que de comprimentos S e L, dispersos aleatoriamente na superfície. Ou para resumir, enquanto a maioria das pessoas tem dificuldade de calcular 20% de 35% de R$215,00 reais, formigas conseguem calcular A = 2SL/pN!

“Os resultados de nossos estudos, de que formigas individuais podem fazer avaliações precisas das áreas de nidificação com base em uma regra de ouro, mostram de uma forma única como animais usam algoritmos robustos para tomar decisões quantitativas bem embasadas”, concluiu a dupla. E vamos concluir, por enquanto, o assunto de formigas.

Como disse, essa descoberta passou desapercebida por provavelmente quase todo mundo. Afinal mais insetos ou animais fazendo coisas que envolvem matemática são chatos. Vamos voltar ao mundo real!

He say one and one and one is three, Got to be good looking, Cause he’s so hard to see

Todos sabemos – ou deveríamos saber – que a Bíblia é uma colcha de retalhos literários. Vários autores, que escreveram ou compilaram textos por séculos e que posteriormente foram unidos em um único pacote. Alguns livros sugerem seus autores, outros não; um exemplo é o Livro de Reis.

Tendo em vista todas as evidências à nossa disposição nos dias de hoje, o melhor que podemos fazer é atribuir este livro da Bíblia a um autor/compilador anônimo do século VI a.C. Não há como afirmar se ele era um profeta ou não, mas muito provavelmente o livro foi composto na Palestina entre a queda de Jerusalém (587/586 a.C.) e o decreto do rei Ciro da Pérsia, que permitiu que os hebreus retornassem à sua terra natal (539 a.C.). A data de 550 a.C. parece razoável para o registro Reis concluída.

O livro foi escrito para os judeus que tinham testemunhado a catástrofe de 587, e para os seus filhos, cuja fé estava oscilando. Ele tinha como objetivo instruir e incentivar, para extrair-lhes os atos de arrependimento por seus pecados passados e para renovar as suas esperanças para o futuro. Foi escrito, em suma, para responder às perguntas angustiantes levantadas pelos acontecimentos de 587.

Mas o interessante deste livro bíblico é uma passagem que pode ser encontrada hoje em 1Reis 7:23:

“Hirão fez também o mar de bronze, que tinha dez côvados de uma borda à outra, perfeitamente redondo, e com altura de cinco côvados; sua circunferência media-se com um fio de trinta côvados.”

Este mesmo versículo aparece também em outros cantos da Bíblia, como em IICrônicas 4:2, onde indica uma série de especificações para o Grande Templo de Salomão. E por que essa passagem é tão interessante?

O texto afirma que foi construído algo que era um “círculo perfeito”. De uma borda à outra 10 unidades de media. Logo o raio tinha 5 unidades. A circunferência tinha 30 medidas. Isso nos mostra que um texto datado de 550 a.C. colocava a razão entre a circunferência e o raio de um círculo perfeito em 3. Ou para ser mais claro, a Circunferência deste círculo perfeito é igual a duas vezes o Raio, vezes 3. C=2.R.3.

Lembra-se da época da escola? Provavelmente você fazia o mesmo cálculo usando símbolos mais complicados como C=2πR. Essa letra grega ai no meio é o PI. Compare as duas expressões, a sua e a da Bíblia, e você vê que para os judeus antigos π=3.

É muito fácil perceber este erro hoje, se é que alguém pára para pensar nisto, mas na época do Antigo Testamento era normal, e tudo culpa das bolas – ou círculos, se preferir.

Ninguém sabe ao certo o que fez com que as pessoas desejassem medir as coisas. Curiosidade, inveja, exibicionismo. . . mas o certo é que tão logo que foi percebido que se poderiam ser cobrados impostos de outras pessoas, simplesmente por possuírem um pedaço de terra, a arte de se medir foi elevada a novos patamares, nasciam os primeiros geômetras profissionais. Logo perceberam que se medir quadrados, retângulos, paralelogramas, triângulos era brincadeira de criança, mas quando surgiam curvas a coisa complicava. O que fazer?

Bem talvez pegando um círculo, que parece à primeira vista como a forma mais simples de curva, pudéssemos tirar algum segredo dai. Um círculo é composto de algumas partes básicas: um centro, um raio, um diâmetro, uma circunferência e uma área. O centro é o centro. O raio é a distância do centro até a borda do círculo. O diâmetro é a largura do círculo (que calha de ser igual a duas vezes o raio). A circunferência é a medida da borda e a área a parte de dentro. Como essas partes estariam relacionadas uma à outra? A relação raio diâmetro era bem simples. A área do círculo estava relacionada à circunferência. Qual a relação do raio (ou do diâmetro) com a circunferência?

Uma pergunta simples, uma pergunta cuja resposta chegou a beirar e ultrapassar a loucura ao longo da história.

Como descobriram o Pi? De onde ele vem? Bem, deixando gênios de lado, suponha que nosso antepassado primitivo tivesse a curiosidade de pegar um barbante, amarrar em um prego, fincar o prego no chão ou em uma tábua e com um giz preso na outra extremidade desenhar um círculo pode ter chegado a uma descoberta interessante: se depois de traçar o círculo soltasse o barbante – que teria o tamanho do raio do círculo – e começasse a colocá-lo sobre a linha traçada, marcasse onde ele chegava e colocasse de novo na continuação e de novo e de novo, com 6 operações dessas o barbante daria a volta completa! Voilá! Se você multiplicasse o raio por 6, teria a circunferência da figura! Ou então se multiplicasse o diâmetro por 3! Trabalho resolvido. Existe uma lei da natureza que afirmava que a circunferência de um círculo era igual a duas vezes o raio do círculo vezes 3. Mas o que era esse 3? O que importa! A conta dá certo.

Isso, é claro, se você não precisar ser MUITO preciso.

Isso explica a passagem Bíblica do livro dos reis. Se você usasse algum método de medição mais “físico” como cordas para se medir as coisas, chegaria numa aproximação muito boa. Para se ter uma idéia, nos século XII a.C. – quase 700 anos antes de escreverem o Livro de Reis – os chineses também arredondavam Pi para 3.

Mas de novo, o que é Pi? Por que alguém desejaria saber o valor de Pi?

Voltemos ao imposto de renda. Suponha que você comprou um terreno perto do mar e construiu um farol. O coletor de impostos precisava cobrar de você o espaço de terra que você estava usando. Como ele iria fazer isso? Para descobrir a área do circulo ocupado por sua construção ele precisaria conhecer a circunferência do seu farol. Ou suponha que você construísse carroças, e descobrisse que ao se colocar uma tira de metal ao redor das rodas de madeira, elas durariam muito mais. Ou que você construísse barris. Ou faróis, piscinas ou qualquer coisa redonda que não fossem buracos. Você teria que trabalhar com a borda, saber quanto de metal usaria nas rodas, ou nos aros para segurar os barris, ou em pedras para a borda da piscina. Lembre-se, eles eram nossos antepassados, mas também tinham orçamentos. Assim a forma mais rápida de se calcular o quanto teria a circunferência era multiplicar o diâmetro do círculo por 3. Esse número não tinha um nome, era uma medida prática de se trabalhar com círculos.

O problema começava a surgir quando você resolvesse pegar papel e lápis, porque ai notava que esse “3” não era exatamente exato. Se você precisasse ser extremamente preciso notaria que a tira de metal, que você encomendou baseada nas medidas que seu estagiário calculou, não se enrolava com perfeição ao redor da roda da carroça. Faltava um pouco de metal para ela se fechar perfeitamente. Ficava um pedacinho, bem pequeno, sem metal. Mas tudo bem, isso não afetaria o funcionamento da roda. Quem se importaria com essa diferença mínima?

Bem. Os babilônios se importavam. Os egípcios se importavam. Os babilônios conseguiram com seus cálculos descobrir que a razão entre a circunferência e o diâmetro do círculo não era de exatamente 3, e sim de 3.125. Os Egipcios – muito mais exagerados – usavam uma razão de 3.1605. E isso lá pelos idos de 2000 a.C.

No caso egípcio, encontramos uma menção a este número no Papiro de Ahmes – ou Rhind – mostrado como uma fração: 4x(8/9)^2, que se encontra no Papiro de Ahmes ou Rhind, gravado no segundo século a.C.. É este valor que se obtém experimentalmente, medindo a circunferência de latas, pratos e cestas e dividindo-a pelos diâmetros respectivos.

Já, para os Babilônios, o valor 3+(1/8) é encontrado em uma das Placas de Susa, o único exemplo conhecido nessas épocas do que parece ser uma familiaridade com um processo geral que, em princípio, permite determinações tão exatas quanto se queira.

Inclusive, depois de anos medindo e desmedindo as pirâmides do Egito, John Taylor propôs a idéia, em 1859, de que a grande pirâmide não era apenas uma construção sinistra e gigante no meio do deserto. Ao se dividir o perímetro da Grande Pirâmide de Khufu pela sua altura, o resultado se aproximava muito de 2.Pi – e ao comparar isso com o fato de que ao se dividir a circunferência de um circulo por seu Raio obtemos 2.Pi, declarou que talvez a Grande pirâmide tenha sido erguida como uma representação da “esfericidade” da Terra.

Legiões de escravos construindo por anos um Pi gigante, holográfico, feito de pedras que pesavam toneladas, no meio do deserto. Eis um baita sonho erótico para muitos matemáticos.

Mas foi quando gregos começaram a se importar com este número que a merda bateu no ventilador.

He say I know you, you know me, One thing I can tell you is, You got to be free

Os gregos antigos eram pessoas interessantes. Punheteiros de primeira linha. Eles não contentavam em se preocupar em porque se você gira um compasso cria um círculo. Eles queriam saber se o círculo era democrata, qual o prato favorito do círculo e que tipo de música ele gostava de escutar. Eles não se satisfaziam com aproximações toscas, eles queriam saber exatamente. Eles levaram a matemática de uma ferramenta prática de comércio e arquitetura para a ciência angustiante, massante, enfastiante e increvelmente maravilhosa.

Entre Arquimedes de Siracusa, no século III a.C.. Arquimedes era famoso por correr pelado pelas ruas gritando palavras gregas e em dizer que sua vara era capaz de abalar a Terra. Arquimedes era tão foda que ele era matemático, físico, engenheiro antes de inventarem números. E ele resolveu estudar esse número, razão entre a circunferência – ou perímetro – e o diâmetro de um circulo. Arquimedes mergulhou de cabeça no problema com expedientes novos, muito mais profundos. Ele se propôs descobrir um processo para a determinação deste número com a precisão que se desejasse.

Se utilizando de polígonos que tocavam um determinado círculo, respectivamente do lado de dentro e de fora, ele calculava a área dos polígonos, que podia ser calculada com exatidão, resultando em um limite superior e outro inferior para a circunferência procurada, pois o polígono externo parece ter uma área maior que o círculo, e o interno, um menor.

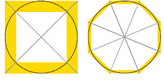
Quanto mais ângulos nos polígonos, mais próximo do círculo se chegaria. Arquimedes chegou ao polígono de 96 lados, através do qual obteve a seguinte aproximação:

3.1410 < p < 3.1428

Uma aproximação muito boa. Mas que infelizmente trouxe um terrível efeito colateral. Hoje quando ouvimos falar de caixa de Pandora, imaginamos que se trata de uma simples lenda, ou uma metáfora. Estudando a história de Pi eu acredito em segredo que a origem desta tragédia foi a matemática, e o círculo.

Assim que começaram a comparar polígonos com círculos os gregos libertaram no mundo uma maldição muito maior do que o simples cálculo da razão do perímetro do círculo.

Em algum momento um daqueles gregos pensou: se eu tenho um quadrado, consigo medir a área dele. Sabendo como traçar círculos com a área que eu quiser, usando o número mágico, quanto tempo eu levo para traçar um círculo com a mesma área do quadrado? Claro que os gregos possuíam apenas réguas e compassos para fazer isso. Antes de continuar lendo, pense a respeito deste problema. Você acha que consegue pensar em uma solução?

Tantas pessoas foram contaminadas por esta idéia que em 1755  a “Real Academia de Ciências de Paris” decidiu não aceitar mais nenhuma proposta para a solução. Este problema ficou conhecido como a quadratura do círculo, e as pessoas que se envolviam com ele acabavam desenvolvendo Morbus cyclometricus – a doença da quadratura. Essa doença chegou a contaminar desde ilustres desconhecido a figuras famosas como o cardeal Nicolau de Cusa e o filósofo Thomas Hobbes; Hobbes até se mostrou disposto a ignorar as mais crassas contradições de sua proposta na sede de chegar à resposta a tantos séculos esperada, chegando a afirmar que ele estava correto e o Teorema de Pitágoras errado.

Hoje sabemos que a quadratura do círculo não poder ser calculada é culpa de Pi. O número é irracional, portanto, não permite ser expresso pela divisão (fração) de dois números inteiros. Além disso, ele é transcendente, ou seja, não é raiz de nenhum polinômio com coeficientes fracionários cujo resultado seria π. Mas apenas em 1822 isso foi provado, por Ferdinand von Lindemann.

Mas o problema com o Pi, que oficialmente ganhou a nomenclatura de π apenas em 1706 do matemático William Jones, é que ele não se contenta em assombrar apenas círculos. Ele parece estar infiltrado em todas as áreas da nossa vida, nos espreitando e nos assombrando.

No início do século XVIII Georges Louis Leclerc, conhecido pelas mulheres da região como Conde de Buffon, foi uma das vítimas colaterais de π. Aparentemente quando criança, a mãe dele não lhe alertou sobre as crianças famintas da África, então ele desenvolveu um gosto por brincar com comida. Numa bela tarde ele estava sentado em uma cadeira brincando de jogar pães por cima do ombro para trás. O chão era feito de tábuas de madeira e quando se virou ele viu que alguns dos pães estavam em cima das linhas entre as tábuas e outros não. O problema é que além de Conde, Leclerc era matemático, e não tardou a perceber que sua brincadeira representava um problema de probabilidade geométrica, que pode ser traduzido da seguinte maneira:

Dado um objeto mais largo do que alto de largura 4cm – digamos que uma agulha -, quando jogado ao acaso num assoalho feito de tábuas de 4 cm de largura, qual a probabilidade de que a agulha caia atravessando uma das junções?

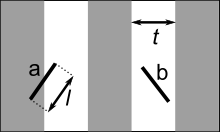
Bem, vamos considerar que X é a distância entre o centro da agulha e a junção mais próxima. Não é difícil constatar que nesse caso que X pertence ao intervalo [0, 2].

θ como o menor ângulo entre a agulha e uma reta perpendicular as junções.

Então, nesse caso θ pertence ao intervalo fechado…

Bem, resumindo a parte chata (caso queiram esclarecimentos da parte chata nos mande um e-mail), temos que a resposta é igual a 2/Pi. Quanto mais agulhas você atirar, mais perto de 2/Pi você chega. Em 1901 outro matemático, desta vez italiano, Mario Lazzarini, afirmou ter atirado uma agulha mais de 3400 vezes e obteve um valor de π igual a 355/113 – ou  3.1415929, que se afasta do valor real em menos de 0.0000003. Claro que quando paramos para pensar em como ele conseguiu atirar uma agulha mais de 3400 vezes de forma realmente aleatória, começamos a nos lembrar de comentários de outros matemáticos de como Mario trapaceou um pouco em seu experimento.

O escrutínio que teve início com os gregos, resultou em cálculos hoje que determinam π até a 8.000.000.000.000.000 casa decimal. Para se ter idéia do que isso significa em 2006, o japonês Akira Haraguchi, enumerou meras 100.000 casas decimais de π, exercício para o qual gastou 16 horas.

Hold you in his armchair, You can feel his disease

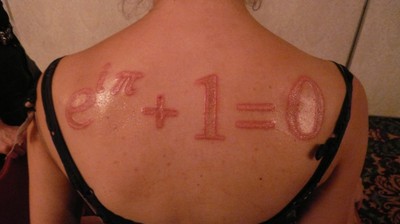
Mas afora isso, por que a fascinação?

Carl Sagan eu seu livro Contato trabalha coma idéia de que encontrarem π a assinatura de Deus. π é uma sequência de números infinita e irracional – uma bela definiçao de Deus, eu diria – e dentro dela estaria escondida tal assinatura.

Peter Boghossian e Richard Dankins discutiram certa vez o que poderia ser uma evidência da existência de Deus e obviamente em determinado ponto Contato entrou na discussão. Em um mail enviado para Peter eu disse que essa seria uma evidência pobre, já que os números de π são aleatórios, poderíamos, com muita paciência, encontrar qualquer padrão dentro dele, existe um site inclusive que localiza seu aniversário dentro de π. Surpreendentemente Peter respondeu o mail com uma questão:

“mas e se esta assinatura dentro de π aparecesse apenas uma vez, sem nunca se repetir?”Isso seria uma evidência?”

π é infinito. E aleatório. Isso esbarra em um problema de nossa mente: contemplar o que é infinito. Por um lado imaginamos que o infinito é algo tão grande que não pode sequer ser pensado. Mas isso não é sempre verdade, Cantor nos mostrou que existem infinitos de diferentes tamanhos.

Pegue uma régua. Ande com o dedo para 1 cm. Ande então metade do caminho, para 1,5cm. Ande novamente metade desta segunda distância – 0.5cm – distância na régua. E novamente metade desta metade. Continue adicionando essas metades infinitamente. Você logo percebe que esta é uma soma infinita, mas você nunca vai chegar no fim da régua. Na verdade você não chega a 3cm. Um infinito menor do que a tampa de uma caneta Bic, que você consegue segurar em sua mão.

Agora de fato, e se dentro de uma série aleatória e infinita surgisse apenas uma sequência uma vez? Pensei comigo mesmo, isso poderia ser feito. Neial Gaiman certa vez disse que todo livro tem um final feliz, basta você saber quando parar de ler. Assim uma sequência única poderia ser encontrada dependendo de quando você decidisse que ela começa e termina, seria uma trapaça.

Como buscar tal assinatura então sem trapaças? Se você está em um navio e ele está afundando, você não enviaria apenas um S.O.S. pelo rádio, no meio da estática eletromagnética da atmosfera apenas um S.O.S. se perderia. Você mandaria vário, a espaços regulares. Eu imagino que qualquer mensagem codificada dentro de π seria como uma sinal, ou uma série de números que se repetiriam sem parar. Um farol piscando na escuridão nos guiando.

Bem… um matemático amador, Hagar Dronbecker , descobriu que Pi se repete no nível hiper- milésimo. A idéia veio a ele enquanto estava comendo um sanduíche de tomate. Aparentemente , o padrão de meta- fractal da listra verde e vermelha dos tomates o levou a inferir que Pi poderia de fato se repetir no nível hiper-milésimo, graças ao fato de que Pi não poderia ser mais aleatório do que quase-repetição da curva de escaleno dos tomates.

Mais especificamente, o ponto de repetição em Pi ocorre quando ele começa a se mover em um conjunto controverso de números que os matemáticos chamam de “números NLNcHT” –  New Large Numbers Considered to be in the Hyper-Thousands ou Novos Grandes Números considerados em hiper-Milhares. A seqüência de repetição encontrada por ele é constituída pelos seguintes números: ” 949700010007949 “. Agora repare a beleza disso, uma assinatura que se repete e não apenas aleatória, mas um palíndromo numérico dentro de π. Um olho que brilha como uma maçã dourada que pode ser lida em ambos os sentidos…

Não seria interessante que houvesse mesmo uma assinatura embutida dentro de um círculo que nos avisasse que o criador nos espera em algum ponto da existência?

Não seria ainda mais interessante se essa assinatura fosse a responsável, de certa forma, por nossa evolução mental?

Até hoje não existe uma explicação racional de porque nossos cérebros se desenvolveram tanto. Em algum momento da história um catalizador fez com que parássemos de lamber nossas bolas e assássemos a medía-las, e medindo-as encontramos π, nos esperando.

Hanne Tügel já me disse certa vez que “dito de modo crasso, pi significa a colisão entre a inteligência humana e a Matemática”. Mas e se ele fosse mais? E se π estivesse já dentro dos seres mais simples, se fizesse parte da vida e de alguma forma estivesse esperando que alguma mente o questionasse para que ele respondesse, fazendo-a evoluir conforme ouvisse sua resposta?

Claro que esta é uma suposição tola. Afinal como afirmar que π está presente nas formas mais simples de vida esperando ser descoberto? Para afirmar isso eu teria que ter evidência que animais com cérebros estupidamente mais simples do que nós poderiam ter a mesma facilidade que temos para trabalhar com π nos níveis mais básicos da vida certo?

Come together, right now, Over me

por LöN Plo

Conheça as vantagens de se juntar à Morte Súbita inc.