Este texto foi lambido por 38 almas esse mês
Senso Numérico
Senso numérico é o nosso nome para aquela “intuição” com os números — uma habilidade de perceber relações e visualizar, de forma completa e clara, que os números são apenas símbolos que representam situações reais. Eles não têm vida própria, a não ser como parte de um jogo.
Quase todos nós detestávamos aritmética na escola. E a maioria de nós ainda a considera uma tarefa árdua.
Há duas razões principais para isso. A primeira é que geralmente nos ensinaram a resolver problemas do jeito mais difícil e demorado — porque era o jeito mais fácil de ensinar. A segunda é que os números frequentemente parecem absolutamente frios, impessoais e estranhos.
W. W. Sawyer expressa isso assim em seu livro Mathematician’s Delight:
“O medo da matemática é uma tradição herdada dos tempos em que a maioria dos professores sabia pouco sobre a natureza humana e nada sobre a natureza da própria matemática. O que ensinavam era uma imitação.”
Por “imitação”, o Sr. Sawyer quer dizer a repetição mecânica de regras, a memorização de tabuada de adição ou multiplicação sem qualquer compreensão das verdades simples que estão por trás disso.
Na vida real, claro, nunca lidamos com um número quatro abstrato. Lidamos sempre com quatro tomates, ou quatro gatos, ou quatro reais. É apenas para aprender a lidar de forma prática com os tomates, os gatos ou os reais que praticamos com um quatro abstrato.
Nos últimos anos, professores de matemática começaram a demonstrar preocupação com a compreensão popular dos números. Alguns avanços foram feitos, especialmente no ensino de frações com diagramas e barras coloridas de diferentes comprimentos para ajudar os alunos a visualizar as relações.
Mas, quanto aos métodos de resolução de problemas, muito pouco foi feito. A maior parte do ensino ainda apresenta métodos contrários à rapidez e à facilidade no uso dos números.
Quando ensinei meu filho a tabuada de multiplicação, há um ano, por exemplo, fiquei horrorizado com a forma como ele foi instruído a recitá-la. Eu havia criado alguns cartões de memória (flashcards) e estava tentando treiná-lo a “ver apenas a resposta” — uma técnica básica de matemática rápida que será explicada nas próximas páginas. Ele hesitava, claramente desconfortável. Até que finalmente revelou o problema:
“Na escola não me deixam fazer desse jeito, papai,” ele disse. “Eu não posso olhar pra 6 x 7 e simplesmente dizer ‘42’. Eu tenho que dizer ‘seis vezes sete é quarenta e dois.’”
Esperamos que isso mude em breve — não menos que três diferentes grupos profissionais de professores de matemática estão reavaliando os métodos atuais de ensino — mas, enquanto isso, nós que aprendemos dessa forma temos que começar de onde estamos.
Relações
Embora a aritmética só seja realmente útil para nos servir no trato com objetos concretos — sejam ações da bolsa, vacas, colunas de jornal ou quilowatts —, o fato de o mesmo sistema numérico básico se aplicar a todas essas coisas permite que isolemos o “número” do “objeto”.
Isso é, ao mesmo tempo, a beleza e — pelo menos para as crianças na escola — o terror da aritmética. Para entender plenamente sua aplicação, estudamos a matemática como algo à parte.
Para fins de prática, por hora, esquecemos os tomates e pensamos no conceito abstrato de “4” como se ele tivesse uma existência real. Claro que ele só “existe” no método de pensar sobre as ferramentas chamadas “números”, que fomos construindo lenta e cuidadosamente ao longo de milhares de anos.
Há aqui espaço apenas para tocar brevemente nos fascinantes resultados do fato de termos nascido com dez dedos e, por isso, usarmos o dez como base de nosso sistema de contagem. Outros sistemas já foram e ainda são usados — desde o sistema binário, baseado em dois, usado por computadores digitais, até o sistema duodecimal (base doze), ainda utilizado na compra de ovos, produtos vendidos em dúzias, no sistema monetário britânico, em polegadas por pé e em horas por dia.
Nosso sistema de contagem é baseado no 10, porque temos 10 dedos. Refinado e aperfeiçoado ao longo dos séculos, ele é um sistema maravilhoso.
Tudo que você precisar fazer em aritmética — seja calcular o concreto necessário para construir uma barragem ou conferir se não está sendo cobrado a mais por um frango de 1,6 kg a 49½ centavos por libra pode e será feito dentro da estrutura do dez.
Um exercício surpreendentemente útil para desenvolver uma intuição com as relações entre os números que compõem o dez é passar alguns momentos com o seguinte exemplo simples.
Primeiro, olhe para estes três pontos:
(• • •)
Nada muito empolgante até agora. Mas agora acrescentamos mais três pontos, logo abaixo deles:
(• • •)
(• • •)
Quantos pontos há agora? Seis, claro. Mas como chegamos a seis? Adicionamos três pontos aos primeiros três. Então quanto é três mais três?
Você certamente sabe a resposta, e isso pode parecer idiota, até óbvio demais. Mas há algo poderoso aqui.
Também dobramos o número inicial de pontos? Havia três, e adicionamos a mesma quantidade. Agora há seis. Então, quanto é três mais três, de novo? E quanto é duas vezes três?
Você sabe a resposta, mas pare por um momento e tente visualizar os seis pontos. Eles representam, ao mesmo tempo, “três mais três” e “duas vezes três”. Quanto melhor você conseguir sentir emocionalmente essa relação — quanto mais firme for essa sensação, além da compreensão racional — mais rápido e fácil será o restante deste livro.
Agora, vamos adicionar mais três pontos:
(• • •)
(• • •)
(• • •)
Quantos pontos temos agora?
Quanto é três vezes três? Você consegue sentir isso? Quanto é seis mais três? Dê uma pausa antes de responder, para deixar a resposta se fixar na mente.
Qual é um terço de nove?
Brinque um pouco com esses pontos. Tente ver o maior número possível de relações entre eles. Note que três nonos é igual a um terço. Por quê? Quanto é seis nonos em números mais simples?
Curiosamente, toda a nossa aritmética — mesmo aquela que lida com valores na casa dos milhões — se baseia no número de pontos que você tem agora diante de si. Some um ao nove e você obtém dez — que é a base do nosso sistema de contagem.
Nós expressamos isso com um novo número “1” deslocado para significar uma dezena, e um “0” para indicar o nada — nada além do dez.
Se realmente temos um senso das relações contidas no número nove, estamos muito adiantados no caminho de nos sentirmos em casa com os números.
Pare um pouco aqui e, em seu caderno, desenhe dez pontos. Divirta-se organizando-os em duas linhas de cinco pontos cada. Veja o que acontece se tentar organizar o mesmo número de pontos em um número diferente de linhas, com o mesmo número de pontos em cada linha, de forma que o total continue sendo dez.
Volte a olhar para as duas linhas de cinco pontos e veja se consegue “sentir” a razão pela qual conseguimos expressar um quinto e um meio de dez (ou de um) com um número decimal de um único dígito — mas não conseguimos fazer isso com um terço ou um quarto.
Ver Apenas a Resposta
Além de desenvolver um “senso” para relações numéricas, existem certas regras específicas de procedimento que vão acelerar seu trabalho com números.
A primeira delas é simplesmente uma questão de treino. Um treino totalmente novo para muitos de nós, e diretamente oposto ao modo como a aritmética costuma ser ensinada — mas que, sozinho, já oferece uma melhora impressionante.
A técnica consiste em ver apenas a resposta.
Ao somar, aprendemos a “ver” os dígitos 4 e 3 como 7 — e não como 4 e 3.
Depois, ao multiplicar, aprendemos a “ver” os dígitos 4 e 3 como 12 — e não como 4 e 3.
Isso pode parecer elementar. Talvez você já esteja fazendo algo parecido ao lidar com números. Mesmo assim, um pouco de esforço consciente nessa direção trará grandes resultados.
Tente se lembrar, se puder, de como foi quando você aprendeu a ler. Você soletrava cada palavra, letra por letra. Era lento, difícil, e nem um pouco prazeroso. Mas hoje, você reconhece palavras e frases inteiras num piscar de olhos. E isso não só é mais rápido, como também muito mais fácil.
Infelizmente, isso é o oposto do que se ensina em aritmética, então a maioria de nós precisa desaprender o que foi imposto na escola. Mas vale o esforço — e é essencial para muitos dos métodos ágeis e atalhos que virão mais adiante neste livro.
A aritmética já foi chamada de “a linguagem dos negócios”. E, em muitos sentidos importantes, ela realmente é. Para entender balanços financeiros, receitas e despesas, é preciso ter um bom domínio da linguagem matemática. Nossa ênfase em ver apenas a resposta — em ver 6 x 7 como 42 — é a base de um vocabulário matemático. Os métodos e atalhos que virão depois poderiam ser chamados de gramática, mas a gramática é inútil sem vocabulário.
Ao longo deste livro, de vez em quando vou inserir pequenos exercícios casuais de prática em ver apenas a resposta. Por favor, não os ignore. Eles são importantes. Influenciam diretamente todos os outros elementos do livro.
Some estes números: 8 7 6
Você viu os dígitos 8, 7 e 6? Provavelmente você foi ensinado a somar dizendo “8 mais 7 é 15; 15 mais 6 é 21.” Isso é muito lento.
Em vez disso, pratique olhar para o 8 e o 7 e pensar, automaticamente, “15”. Tente fazer isso sem dizer ou pensar nem o 8 nem o 7. Depois, pensando apenas em “15”, olhe para o 6 e veja “21”. Você não precisa dizer nem pensar “6”.
Se nunca tentou isso, a ideia pode parecer não apenas nova, mas até um pouco chocante. Mas você se acostuma bem rápido se praticar — e isso já acelera bastante o raciocínio com números, mesmo sem usar outras técnicas. Não é difícil. Só exige um pouco de prática, e conhecer bem a tabuada de adição, para não ter que forçar a memória e lembrar quanto dá 8 + 7. É como quando você olha para as letras “m” e “e” e lê “me”, sem precisar formar a palavra conscientemente.
Tente de novo: 8 7 6
Agora, pratique as adições a seguir tentando ver apenas a resposta. Não diga, nem pense nos dígitos que está somando. Faça o possível para “ver” 4 + 5 como 9 — e não como “4 mais 5”. Leia as respostas dessas somas da mesma forma que você lê “i” e “t” como “it” em inglês, e não como duas letras separadas.
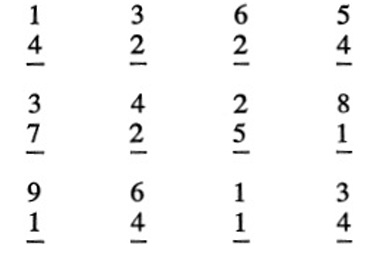
Se você começou a ver apenas as respostas, ótimo. Se não, talvez seja útil tentar novamente.
Trabalhe com Números, Não com Algarismos
O segundo passo para desenvolver um verdadeiro senso numérico vai ainda mais longe na construção de uma habilidade natural e confiante com números. Esse passo é muito mais radical do que ver apenas a resposta. Ele contraria praticamente tudo o que normalmente nos ensinam sobre números — mas você logo verá como isso faz sentido e o quanto pode ser importante.
Essa regra, aceita por praticamente todos os professores de matemática rápida, é:
trabalhe da esquerda para a direita — e não da direita para a esquerda.
Isso é exatamente o oposto do que se ensina na escola. Lá, somos ensinados a somar, subtrair e multiplicar da direita para a esquerda. É mais fácil de ensinar às crianças e mais fácil de aprender dentro da abordagem “imitativa” de aprendizado por repetição — mas é totalmente contrário à forma como lê-se e pensa-se sobre números.
Existem pelo menos três vantagens importantes em trabalhar da esquerda para a direita:
-
É assim que lemos tudo em uma página. Lemos da esquerda para a direita.
-
É assim que lemos um número — até o momento de fazer algo com ele.
Por exemplo, observe o número 164.928. Você o lê como “cento e sessenta e quatro mil, novecentos e vinte e oito”. Mas, quando começa a somar, subtrair ou multiplicar, lhe ensinam a lidar com ele como 8, 2, 9, 4, 6, 1.
Ou seja, não é mais o mesmo número. Logo no início, você é instruído a combiná-lo com outro número numa forma totalmente estranha e irreconhecível.
-
Trabalhar da esquerda para a direita permite lidar com os valores mais importantes primeiro, e só depois com os “detalhes”.
Imagine que você é um vendedor e acabou de fechar uma venda de R$ 423, da qual receberá 6% de comissão. Se você trabalha da esquerda para a direita (você aprenderá como, mais adiante), já com o primeiro dígito você sabe que sua comissão será algo em torno de vinte e poucos reais. Com os dois primeiros dígitos, você já sabe que será R$ 25 e alguns centavos.
Mas, se você usa o método escolar, da direita para a esquerda, os dois primeiros dígitos que você calcula revelam apenas os centavos. Você só sabe que vai receber algo com 38 centavos. Só ao terminar todos os cálculos é que você descobre que sua comissão será de R$ 25,38.
Esses R$ 0,38 podem ser importantes para o contador, mas em relação ao número em si, são detalhes. Você se importa muito mais com os R$ 25 do que com os R$ 0,38.
Isso vale para qualquer número e qualquer aplicação, com ou sem vírgula decimal. O primeiro dígito de um número é dez vezes mais importante que o segundo, cem vezes mais importante que o terceiro, e assim por diante. Se a venda que discutimos fosse cem vezes maior, você ainda estaria muito mais interessado na parte dos R$ 2.500 da comissão do que na parte dos R$ 38.
Trabalhar da esquerda para a direita revela, passo a passo, os números mais importantes primeiro. Só por isso, os novos métodos que ensinam a fazer isso estão entre as ferramentas de estimativa mais valiosas que você pode ter.
O fato de que cada dígito num número diminui de importância em dez vezes conforme se move uma casa para a direita é a razão pela qual muitas empresas hoje apresentam seus relatórios e resultados financeiros em números arredondados: ignorando os centavos ou, no caso de empresas muito grandes, dezenas, centenas ou até milhares de reais.
É o número à esquerda que importa mais. Até o governo dos EUA agora permite que cada um de nós calcule o imposto de renda com números arredondados — para o real mais próximo em cada dedução e etapa do cálculo. Se sua declaração de imposto for um pouco mais complicada e você mesmo a preencher, e ainda não tentou arredondar os números, ficará surpreso da próxima vez que fizer isso. Economiza quase metade do tempo.
Se alguma técnica neste livro valer mais do que o preço do próprio livro, eu arriscaria dizer que os métodos de trabalhar da esquerda para a direita estariam no topo da lista. Há outras técnicas valiosas, mas essas são absolutamente únicas.
O valor dessa abordagem para o seu senso numérico só vai se revelar à medida que você aprender os métodos que a tornam possível. O ponto aqui é simples: pratique isso. À medida que você aprende a usar essa técnica, a diferença se torna tão clara quanto a de pensar no número 462 — ou abordá-lo como 2, 6, 4.
Converter para Formas Mais Simples
A maioria de nós converte alguns problemas de cálculo para formas mais simples — quando conseguimos e quando percebemos que podemos — sem pensar muito a respeito.
Você não pensaria duas vezes ao tentar descobrir quanto tem em reais, se encontrasse três moedas de 25 centavos na mão. Chamamos 25 centavos de “um quarto de real” porque é exatamente isso — um quarto de um real. Na verdade, se você pegar uma moeda dessas agora, verá que nem sequer está escrito “centavos” nela. A designação oficial é “um quarto de real” [Nota do Tradutor: no texto original, refere-se à moeda de 25 centavos de dólar, cuja inscrição é “quarter dollar”].
Quer alguém tenha te chamado atenção para isso ou não, você está agora pensando em termos de alíquotas. Um capítulo importante virá mais à frente sobre os atalhos que as alíquotas tornam possíveis. Todo esse conceito, uma vez compreendido, é apenas uma extensão e refinamento da sua compreensão instintiva de que 75 centavos é o mesmo que ¾ de um real.
Isso é converter para uma forma mais simples.
Talvez você também já tenha notado que é mais fácil multiplicar 692 por 99 subtraindo um 692 de cem 692’s (ou seja, 69.200 – 692) do que montar o problema inteiro no papel e resolver do jeito clássico, que seria algo assim:
 Qual método é mais rápido e fácil? Ainda que você talvez não tenha percebido, ao usar o primeiro método, você aplicou uma técnica básica e eficiente chamada “arredondar e ajustar”. E ela pode ser aplicada a muitos outros números além do 99.
Qual método é mais rápido e fácil? Ainda que você talvez não tenha percebido, ao usar o primeiro método, você aplicou uma técnica básica e eficiente chamada “arredondar e ajustar”. E ela pode ser aplicada a muitos outros números além do 99.
Isso também é converter para uma forma mais simples.
Ou talvez, ao tentar rapidamente calcular uma gorjeta apropriada para uma conta de restaurante, onde 15% é o padrão, você tenha percebido que pode mentalmente calcular um décimo do valor e depois adicionar metade desse décimo. Por exemplo, em uma conta de R$ 5, você calcularia uma gorjeta de 75 centavos. Um décimo de cinco reais é 50 centavos, mais metade disso (25 centavos), resulta em R$ 0,75 — rápida e facilmente.
É claramente mais conveniente chegar aos 75 centavos dessa forma do que tentar (mentalmente ou rabiscando no verso da comanda) multiplicar 5 por 0,15 da maneira clássica:
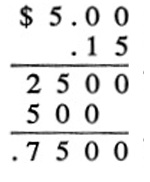 Ainda assim, ao fazer esse pequeno truque, você está simplesmente aplicando uma forma bastante simples do atalho chamado “quebra em partes” (breakdown).
Ainda assim, ao fazer esse pequeno truque, você está simplesmente aplicando uma forma bastante simples do atalho chamado “quebra em partes” (breakdown).
Há outras formas úteis de conversão, como fatoração e variação proporcional. A aplicação desses métodos ao senso numérico ficará clara à medida que você os aprender e começar a utilizá-los.
Os Quatro Passos para o Senso Numérico
Aqui está, para uma revisão rápida, o conjunto dos quatro pilares do senso numérico:
-
Pratique ver relações
Como o 5 se relaciona com o 10? E o 3 com o 9?
-
Veja apenas a resposta
Leia 4 + 3 como 7 — e não como “quatro mais três”.
-
Trabalhe da esquerda para a direita
O número 27 é vinte e sete — não “sete, dois”.
-
Converta para formas mais simples
25 centavos são tanto 25 centavos quanto um quarto de real.
99 é 100 menos 1.
15 é 10 mais a metade de 10.
(E muitas outras conversões virão.)
Antes de prosseguir para o primeiro capítulo realmente “prático” deste livro, comece a se preparar para usar o conteúdo, não apenas ler, tentando ver apenas as respostas nas multiplicações a seguir. Lembre-se: 6 x 7 é 42 — e não “seis vezes sete”.

Alimente sua alma com mais:

Conheça as vantagens de assinar a Morte Súbita inc.


 Qual método é mais rápido e fácil? Ainda que você talvez não tenha percebido, ao usar o primeiro método, você aplicou uma técnica básica e eficiente chamada “arredondar e ajustar”. E ela pode ser aplicada a muitos outros números além do 99.
Qual método é mais rápido e fácil? Ainda que você talvez não tenha percebido, ao usar o primeiro método, você aplicou uma técnica básica e eficiente chamada “arredondar e ajustar”. E ela pode ser aplicada a muitos outros números além do 99.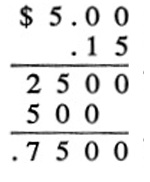 Ainda assim, ao fazer esse pequeno truque, você está simplesmente aplicando uma forma bastante simples do atalho chamado “quebra em partes” (breakdown).
Ainda assim, ao fazer esse pequeno truque, você está simplesmente aplicando uma forma bastante simples do atalho chamado “quebra em partes” (breakdown).