Este texto foi lambido por 404 almas esse mês
Graças a séculos de estudos, de experimentos e à criação de novas tecnologias e ciências, hoje sabemos que por trás da superfície do mundo há leis que governam tudo o que existe. Solte uma maçã e ela cairá em direção ao chão, pise no acelerador de um carro ou chicoteie um cavalo e a velocidade muda. Coloque uma roupa azul e corra na velocidade da luz em direção a alguém e sua roupa ficará vermelha para essa pessoa. Ofereça dinheiro a alguém e a pessoa fará algo para você, cuspa em alguém e sabe como ela reagirá, coloque um espelho diante de um faixo de luz ou um prisma e podemos prever como a luz se comportará.
Vejamos então o exemplo do povo Kariera na Austrália. Eles são uma tribo aborígene, tal e qual às analisadas por Freud para seus estudos sobre tabu e totem. Os Kariera habitam hoje a região leste do continente, originalmente eles ocupavam a área costeira e ilhas próximas de Port Hedland e parte dos rios Yule e Turner. A tribo é composta por aproximadamente 25 grupos, cada um com seu território próprio que variava entre 260 e 320 quilómetros quadrados, cada grupo é composto por mais ou menos 30 nativos.
Como Freud poderia ter suposto, e nós também já que lemos o capítulo anterior, os Kariera vivem com um conceito claro de tabu e totem. Diferente de você, uma pessoa civilizada que apenas segue as leis e bons costumes e possui uma lógica não regida por superstição.
A tribo é dividida em 4 classes ou clãs, cada um possuindo um totem: os banaka, os karimera, os burung e os palyeri. O incesto é um dos maiores tabus tribais, obviamente os aborígenes não sabem que os relacionamentos consangüineos nos afetam no nível cromossômico deteriorando nossos genes, mas o tabu está presente. Como forma de deixar claro o horror ao incesto eles substituem o parentesco consangüineo pelo parentesco totêmico. Isso funciona da seguinte maneira, não importa que você tenha nascido de Maria e José e na barraca do lado uma bela garota tenha nascido de Walter e Simone, e não importa que nem Walter nem Simone tenham qualquer antepassado em comum com Maria e José; para evitar confusões todo mundo sob o mesmo totem é parente, e se você se envolver com sua vizinha será considerado incesto.
Assim os Kariera criaram regras rígidas que regem o relacionamento dos membros da tribo. Lembre-se uma mesma tribo tem quatro totens diferentes. Os indivíduos não tem liberdade de escolha de seus futuros esposos e esposas, eles tem que seguir as regras:
1. Um banaka só pode se casar com um burung.
e
2. Um karimera só pode se casar com um palyeri.
Isso parece uma certa contradição de início, pois se um banaka só pode se casar com um burung, seus filhos não estarão sob o mesmo totem? Não haverá chance de incesto com o tempo?
Para isso eles criaram 4 regras adicionais:
3. Os filhos de um homem banaka e uma mulher burung são palyeri.
4. Os filhos de um homem burung e uma mulher banaka são Karimera.
5. Os filhos de um homem karimera e uma mulher palyeri são burung.
6. Os filhos de um homem palyeri e uma mulher Karimera são banaka.
Desta forma não apenas as pessoas não tem plena liberdade de escolher com quem passarão e vida e terão filhos, mas seus filhos já nascem também “marcados”, com escolhas pessoais limitadas por sua ascendência, que por sua vez foi limitada pela ascendência dos pais e por ai a fora no passado até quando os primeiros Kariera criaram suas leis de relacionamento. Curiosamente este é o tipo de comportamente primitivo que muitos esperam de tribos não civilizadas. Na verdade não há como comparar o sistema de relacionamento dos Kariera com a nossa vida prática dos dias de hoje. Por mais que se mostre o tipo de permutações que esta prática pode gerar e como isso pode diminuir a chance de parentes de sangue terem filhos com guelras. Homens e mulheres ocidentais contemporâneos podem escolher com quem se casar e seus filhos também poderão, embora curiosamente sempre “escolham” alguém da mesma classe social, etnia e que sejam geograficamente próximos.
Somos obrigados a concordar com o comentário. Tirando uma certa nota de racismo, homofobia e outros preconceitos, somos todos livres para levar quem quisermos para jantar com nossos pais. Psicologia tribal é algo muito simples de se compreender, mas vivemos, felizmente, em uma sociedade mais complexa e livre.
Contudo, se de fato pensássemos assim, este texto não existiria. Este tipo de pensamento apenas mostra o quão longe da realidade você está. Não estamos falando de com quem um Kariera pode ou não casar. Como dissemos, hoje sabemos que existem leis que regem tudo o que existe, mas por trás dessas leis, existe um outro nível de absolutos que são muito mais profundos. Um decote, se preferir, que nos revela uma Matriz muito mais pura que rege todas as leis da ciência, e olhando por este decote das leis do universo, podemos começar a entender as algemas e grilhões que carregamos.

um decote de verdade
não uma folha de papel dobrada como esta.
Alguns séculos atrás, na tentativa de desvendar as leis que nos aprisionavam em nossa existência, era comum usar analogias com coisas mundanas, como o jogo de xadrez – já que isso mostrava para as pessoas algo que elas compreendiam e também que o criador da analogia era alguém mais esperto do que elas, pois sabia jogar xadrez.
“O tabuleiro de xadrez é o mundo, as peças são os fenômenos do universo, as regras do jogo são o que chamamos de leis da Natureza. O jogador do outro lado está oculto para nós. Sabemos que seu jogo é sempre imparcial, justo e paciente. Mas também sabemos, à nossa custa, que ele nunca deixa passar um erro nem dá a menor margem para a ignorância”
Quem escreveu isso foi o buldogue de Darwin. Não um cão. O biólogo Thomas Henry Huxley.
O problema é que não queremos meramante apontar quais as regras do jogo e sim aquilo que faz o tabuleiro existir da forma que existe e o porquê das regras do jogo se comportarem da forma que o fazem. Queremos ir além disso. E para fazer isso temos que parar de olhar para fora e olhar para dentro.
Aparentemente as diferentes “leis da Natureza” lidam com coisas distintas. A hidrodinâmica com a natureza dos fluídos, a psicologia com a natureza da mente psíquica, o eletro-magnetismo com as ondas eletro magnéticas e assim em diante. Podemos inclusive criar uma árvore simplificada para mostrar de onde brota nosso destino.

Mas se acreditamos que existe mesmo uma Matriz a quem até mesmo as leis da natureza devem se curvar, devemos mergulhar para dentro de seu decote e não simplesmente nos contentarmos com as formas que suas roupas assumem quando modelam seu corpo. Para evitar confusões filosóficas e associações com megaproduções cinematográficas de ficção científica, de agora em diante nos referiremos a esta Matriz apenas como “Ela”.
Não usaremos tãopouco sua fantasia popular conhecida como “Deus”. Este termo já está historicamente carregado de preconceitos e supertições que atestarão contra a pureza que buscamos. Jeová é, afinal, um totem assim como todos os outros deuses e deusas. Afinal, ‘Ela’ já estava por ai muito antes de Deus ou dos deuses surgirem. Se quiser pode considerar “Ela” como uma divindade suprema, mas apenas no sentido que Spinoza e Einstein sugeriram ao termo. Para entender porque optamos pelo gênero feminino consulte nossa obra póstuma: “Metafísica dos peitos, peitinhos e peitões.”
Pare um pouco para pensar. Você não precisa conhecer nada de hidrodinâmica, de gravitação ou química para saber o que acontece em Vênus, quando chove por lá. A chuva cai, e molha. E você não precisa saber que lá chove uma mistura de chumbo e enxofre para isso. Você sabe disso porque quando chove aqui a chuva cai e molha. Da mesma forma, os cientistas podem dizer do que o Sol é feito sem nunca ter ido lá porque sabemos que um átomo de hidrogênio se comporta lá da mesma forma que se comporta aqui e da mesma forma que se comporta em Alfa-Centauri – e o que é mais incrível: não importa se eles estudam esses átomos de pé ou plantando bananeira. Isso que as pessoas chamam de “leis da natureza” são “princípios” que se comportam de forma simétrica, são as mesmas no universo todo. Da mesma forma que sabemos como vai se comportar uma pessoa em qualquer lugar do mundo caso você dê um tiro no rosto dela, podemos saber o quanto vamos pesar em diferentes planetas, pois mesmo que tenham gravidades diferentes, já que sabemos que a dependência da força da atração gravitacional em relação à massa e ao raio de qualquer lua ou planeta ou estrela ou asteróide ou cereja, será exatamente a mesma dependência da força de atração gravitacional da Terra em relação à massa e ao raio de nosso planeta. Já que todas essas leis, e tudo o que criam está sujeito a essa simetria, podemos então usar a simetria como ferramenta para decifrar a nossa própria natureza.
Mas como fazer isso de maneira simples, sem contas, equações e coisas chatas? Simples. Pare novamente para pensar: por que um espelho apenas troca o seu lado direito com o seu lado esquerdo? Por que ele não troca o seu lado de cima com o seu lado de baixo?
Enquanto pensa nisso vamos falar de um grupo. Quando você abre a sua gaveta de cuecas ou enfia a sua mão dentro da bolsa, encontra uma série de objetos certo? Isso é um conjunto. Um conjunto pode ser formato de infinitas coisas, como por exemplo uma perna mecânica, todas as suas figurinhas do pokemón, as cartas de mulher pelada que você roubou do seu primo, uma barrinha de cereais e um batom. Um conjunto é apenas um amontoado de coisas que segue algum princípio pré estabelecido – por exemplo “tudo que tem dentro da minha bolsa”. Grupos, por outro lado, são diferentes. Pense no Led Zeppelin, quando Boham morreu o grupo acabou, já que ele não poderia ser substituído. O Metallica, por outro lado, quando perdeu Cliff Burton o substituiu por Jason Newsted, um ótimo baixista, mas que aguentou apenas mais um album – depois do “…And Justice for All” lançaram o album preto que já mostrava o luto pela morte do grupo e serviu como semente para o maior e mais ambicioso projeto do novo “Metallica”, o lançamento do movimento Emo, mas isso é outro assunto.
Estes dois exemplos servem para dar uma idéia clara de que um grupo, diferente de um conjunto, precisa ter algumas regras claras para se definir:
1. Ele tem que ter FECHAMENTO: o resultado da combinação de dois membros quaisquer por uma operação deve ser um outro membro do próprio grupo.
2. Ele deve possuir ASSOCIATIVIDADE: se você combinar três membros de um grupo, não importa a ordem, terá como resultado outro membro do grupo.
4.Ele deve possuir um ELEMENTO NEUTRO: um elemento que quando combinado com qualquer outro membro, deixa esse segundo inalterado, é como se ele fosse o baixista do U2, um elemento nulo.
5. Ele deve possuir um INVERSO: para todo e qualquer membro do grupo deve haver outro membro que seja seu inverso e quando combinado com esse inverso ele deve produzir o elemento neutro.
Complicado? Calma, vejamos um exemplo.
Pegue o conjunto dos números inteiros, que vai de -infinito e passa por -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 e vai até +infinito. Podemos considerá-lo um grupo?
Se combinarmos os elementos através de adição, por exemplo, 2+3, o resultado é 5, um número inteiro. Se adicionarmos 2 a -3, 2+(-3) teremos -1, outro número inteiro. Então eles apresentam Fechamento.
Se combinarmos três deles, por exemplo, 2 + 3 + 17, não importa a ordem que os coloquemos, o resultado é sempre o mesmo: (2+3)+17 = (5)+17 = 22 da mesma forma que 2+(3+17) = 2+20 = 22 ou ainda (2+17)+3 = 19+3 = 22. Logo eles apresentam Associatividade.
Eles possuem um elemento neutro, que deixa qualquer membro que se combinar com ele inalterado? Qual número inteiro é o equivalente ao baixista do U2, se é que alguém se lembra do nome dele? Quanto é 1+0? 1! O zero é o elemento neutro.
Eles possuem um inverso? Claro, o inverso de qualquer número é ele mesmo com o sinal negativo. O inverso de 4 é -4 e quando combinados temos o elemento neutro, 4 +(-4) = 0
Agora que chegamos neste ponto você deve ter notado uma coisa. E se dividirmos os membros do conjunto dos números inteiros? Teremos frações, que não fazem parte do grupo. Embora 8/4 seja 2, um membro do conjunto, 4/8 resulta em 1/2, que é um número racional. Isso significa que os números inteiros não são um grupo? Não. Significa que para um grupo existir ele tem que obedecer certas regras, e não todas as regras. Devemos observá-lo como seus membros se comportam sob certas óticas; assim, sob a ótica da adição, os números inteiros são um grupo. Para sermos mais técnicos diremos que sob a COMBINAÇÃO da adição os números inteiros se comportam como grupo, e com isso podemos dizer que eles estão submetidos às leis que regem os grupos.
Deixemos a matemática descançar e fumar um cigarro agora.

Homens são indiscutivelmente mais práticos do que as mulheres. Isso é um fato. Imagine que um casal vai viajar e ficar 4 dias longe de casa. Quantas calcinhas uma mulher precisa levar para o básico? (básico é simplesmente usar, não seduzir ou fazer festinhas ou serem reasgadas com os dentes, essas são acessórios extras) Quantas cuecas um homem precisa levar para o básico? (com homens não existem condições, eles só usam a cueca) Uma mulher dirá que, caso não esteja naqueles dias, precisa de pelo menos uma calcinha limpa por dia, logo 4, isso se ela não precisar de uma limpa para dormir e outra para colocar assim que acordar e não passar o dia com uma calcinha “dormida”, logo 8. Um homem diz que se não sofrer um acidente de intestino solto precisa apenas de uma cueca limpa por dia, logo 1.
Por que isso?
Porque homens sabem que uma cueca pode ser usada de quatro formas diferentes e permanecer limpa. Ele só precisa de quatro operações para isso:
Operação 1 = simplesmente pegue a cueca e a vista (para simplificar chamaremos esta operação de I)
Operação 2 = vire a cueca de trás para frente (chamaremos essa de operação X)
Operação 3 = vire a cueca pelo avesso (chamaremos essa de operação Y)
Operação 4 = vire a cueca de trás para frente e então pelo avesso (chamaremos de operação Z)
Isso nos mostra não apenas que homens são mais práticos mas que essas operações formam um grupo. Veja, a operação I é a identidade, você não virar a cueca de nenhum jeito a mantém na mesma forma original e é o mesmo que não fazer nada com ela, você simplesmente a veste. Cada uma das operações é o seu próprio inverso, se aplicarmos a operação 2 a ela mesmo – vire a cueca de trás para frente e então de trás para frente novamente, ela termina como começou como I, que seria o mesmo que você não mexesse nela.
[Pausa Técnica]
Para evitar ficar repetindo aplicar tal operação a tal operação vamos dizer operação 1 seguida da operação 2. E para evitar dizer tal operação seguida de tal operação vamos usar apenas o nome dela – I, X, Y, Z – e o símbolo “•”, que significa “seguido de”. E para finalizar, vamos escrever sempre da direita para a esquerda, como qualquer língua estranha do ocidente. Assim podemos traduzir “se aplicarmos a operação 2 a ela mesmo – vire a cueca de trás para frente e então de trás para frente novamente, ela termina como começou como I” por X•X=I. Da mesma forma que X•Y•Z deverá ser lido como Operação 4 seguida da Operação 3 seguida da Operação 2.
[Fim da Pausa Técnica]
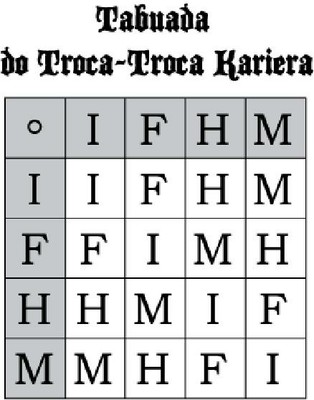
Além de cada operação ser o seu prório inverso, devolvendo a cueca à sua Identidade (sua posição original, dai o I), se combinarmos quaisquer operações o resultado será uma outra operação do mesmo grupo, veja: Z•Y=X já que se virarmos a cueca pelo avesso e a seguir a virarmos de trás para frente e então pelo avesso será a mesma coisa que se simplesmente a virarmos de trás para frente. Para visualizar isso podemos até montar uma tabuada do uso masculino de cuecas na forma de um grupo, veja abaixo:
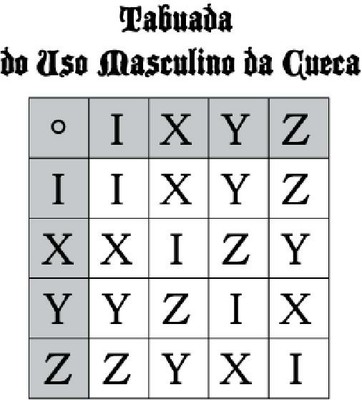
As laterais, esquerda e superior, em cinza são as operações que podemos fazer com a cueca. A bolinha o símbolo de “seguido de”. Assim como uma tabuada de multiplicação, esta nos mostra que qualquer operação resulta em um elemento do grupo, que o grupo tem seu elemento neutro, que não importa a ordem da combinação o resultado é o mesmo e que cada elemento é o inverso de si mesmo. Isso me traz duas coisas à mente neste momento; a primeira o quadrado Sator.
Repare como a área clara da nossa tabuada, a dos resultados, apresenta simetria curiosa. Na primeira fileira de resultados temos a ordem: I-X-Y-Z na última fileira é o inverso: Z-Y-X-I. Repare a primeira coluna: I-X-Y-Z, além de ser a mesma ordem da primeira fileira é o inverso da coluna à direita, que por sua vez é igual à última fileira: Z-Y-X-I. Uma diagonal é formada exclusivamente por identidades I e a outra exclusivamente por operações Z.
A segunda coisa é que assim fica claro porque os homens se destacaram com maior frequência no passado nos estudos da matemática e da física. Usar uma mesma calcinha por quatro dias era e continua sendo tabu. Quem sabem esse tabu desapareça agora e as mulheres busquem suas chances de evoluir e se destacar nas nobres ciências?
Este tipo de simetria por trás das Leis, a simetria d’Ela, está permeada em tudo o que existe, acredite ou não. Mesmo que você não perceba isso. E se você acha que chegar até este ponto do texto foi algo sinistro e trabalhoso, talvez um saco, é só porque você é civilizado e avançado. Os Kariera chegaram a esta mesma simetria por conta própria antes de você nascer. Antes de seus pais nascerem. Antes de sequer inventarem a teoria dos grupos e as equações e fórmulas de simetria.
Vamos traduzir os primitivos em letras, chamemos os
Banaka de A
Karimera de B
Burung de C
Palyeri de D
Se nos lembrarmos das regras conjugais sabemos que um A só pode se casar com um C (e vice-versa) e um B só pode se casar com um D (e também vice-versa), se montarmos uma correspondência familiar (chamaremos de F) podemos dizer que:
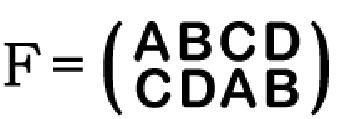
Isso significa que as famílias (F) só podem acontecer com permutações de A e C, B e D, C e A e D e B, veja que dentro dos parênteses as combinações estão de cima para baixo (e vice-versa) e não de um lado para outro, o A está acima do C e assim em diante. Agora repare que se repetirmos a combinação a correspondência familiar F volta a sua forma original:
ABCD – se permuta em:
CDBA – que se permuta em:
ABCD
Então F•F=I, como nas cuecas. O mesmo acorre com os grupos formados pelos filhos dos homens e pelos filhos das mulheres:
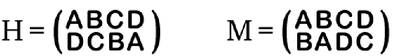
Veja que a relação entre letras continua vertical e que desta vez indicam que os filhos de um homem banaka são sempre palyeri e que os filhos de uma mulher Karimera são sempre banaka. Repare novamente, que como no caso de F, H•H vai ser ele mesmo, o I, como no caso das cuecas. E M•M também = I.
Você já sabe o que vai ver a seguir, certo?
Imagine a complexidade exigida para se fazer com que um sistema desses funcione. Para se criar um Quadrado Sator, tudo o que alguém precisa é paciência. Mas, e para colocar no cerne de sua sociedade 6 regras que consigam oferecer tamanha simetria? Lembre-se que o tabu surgiu muito antes das calculadoras, dos professores, das cervejas e dos deuses.
Essa simetria, que torna os aborígenes australianos exatamente o oposto de “livres” na hora de escolherem com quem fornicar – e fornicação é um de nossos instintos básicos – é tão complexa que não apenas não foi descoberta por nós, homens brancos, europeus e protestantes, até muito recentemente, mas já era usada com eficiência por povos primitivos do outro lado do mundo.
Agora voltemos à questão do capítulo anterior: por que alguém cria uma lei que proíbe algo que não apenas lhe é natural mas é um poderoso instinto? Essa lei deveria ser imposta não pelo próprio ser, afinal se você está feliz e satisfeito transando com sua irmã ou irmão e ninguém ainda disse que isso é errado, de onde viria a lei? Ou para tornar o pensamento menos indigesto veja a coisa assim: suponha que você gosta de comer chocolate, e tem dinheiro para comprar todo o chocolate que quiser, e você se sente bem comendo chocolate, e como tem acesso não come de forma compulsiva, só uma ou duas barras por dia. O que te levaria a decidir que comer chocolate é errado. Ainda mais se não faz nenhum mal para o seu corpo ou mente? No caso do incesto de fato as crianças podem nascer com doenças congênitas da mesma forma que seus filhos poderiam nascer com predisposição à diabetes. Mas como você poderia saber isso se isso se manifestaria em netos e bisnetos que você não estaria nem vivo, ou viva, para ver. E mais! Como afirmar que algo que você tenha hoje foi herdade de seus pais? Lembre-se que os tabus surgiram muito tempo atrás, antes de haver laboratórios para testes de sangue, antes de haver geneticistas para analisar nosso DNA e mesmo antes de terem inventado o papel higiênico. A lei deve ter sido passada a você por alguém que não você, mas alguém que tivesse poder sobre você. Se um Nerd de 30 quilos lhe dissesse para parar de comer chocolate você provavelmente nem daria bola. A fonte do tabu também deve ter controle sobre as pessoas que estão recebendo o tabu.
Devemos supor então que alienígenas vieram à Terra, antes de Deus chegar por aqui, e então açoitaram primatas que nem haviam desenvolvido direito uma linguagem para que adotassem certas proibições como tabus? Que uma raça desconhecida surgisse quando a raça humana ainda mal tapava as vergonhas quando saia para caçar e nos ensinou simetrias de grupos para que passássemos isso para frente na forma de tabus, totens, leis e moral social?
Essa proposta pode agradar alguns Forteanos de plantão, ou fãs de Benitez e Von Daniken. Mas nossa proposta é um pouco mais absurda e radical do que isso; e talvez por isso mais verdadeira.
Imagine que mesmo não percebendo esse sistema anti-livre-arbítrio, ele já está implantado em nós, desde antes de decidirmos descer das árvores. Mesmo antes de decidirmos sair dos oceanos. Mesmo antes de resolvermos respirar. E ele foi programado em uma linguagem que existia momentos antes do universo se formar.
Spinoza afirmava que o livre-arbítrio humano é como uma pedra, pensando que escolhe o caminho que percorre enquanto cruza o ar até o local onde cai. E ele não estava errado. A situação é semelhante a uma poça de água que sente-se livre para ser do formato do buraco em que se encontra. E isso não se aplica apenas a sistemas anti-incesto. Isso se aplica a tudo. Quando você acha que foi a última vez que escolheu livremente qual a marca de refrigerante que bebeu? Ou que sorriu sinceramente para alguém?
Alimente sua alma com mais:

Conheça as vantagens de assinar a Morte Súbita inc.