Este texto já foi lambido por 647 almas.
Entre uma temporada e outra de internação nos hospícios austríacos, um matemático de nome Kurt Friedrich Gödel, fez um rasgo tão profundo na nossa compreensão da realidade que até hoje ela está sangrando. O Teorema da completude de Gödel é a prova lógica de que, em última instância, tanto os cientístas quanto os padres estão todos construindo castelos de sonhos em bases igualmente arbitrárias, e que não existe nem a possibilidade de tentarem provar que suas ilusões são reais. Não há como confirmar se aquilo no que eles acreditam, ou por extensão aquilo que você acredita, é real, certo ou ao menos lógico.
A coisa funcionaria, de forma resumida e simplificada, da seguinte forma.:
Imagine que você está lendo isso logo antes do almoço, naquele dia que não conseguiu tomar seu café da manhã, nem comprar aqueles pacotes de bolacha de R$ 1 real para ficar beliscando. O tempo vai passando e a fome vai aumentando, até que você começa a se incomodar com aqueles banneres de sites de compra coletiva que mostram macarrons, sushis e cortes de picanha ao ponto. Neste momento, que a fome se torna uma sensação física para você eu te desafio: me prove que está com fome! Claro que você pode dizer “me traga comida e eu te mostro!”. Mas então eu me lembro de certas vezes que depois de jantar surge alguém querendo sair para papear e ivariavelmente o papo se desenvolve em um restaurante ou bar onde porções ou pratos são pedidos, e mesmo estando satisfeito eu comi, e comi bem. Também me lembro de um sobrinho que é capaz de comer feijoada até passar mal, literalmente, para 15 minutos depois sair pedindo comida porque está com fome. Também me lembro de uma conhecida que quando tem muita fome não consegue comer nada porque fica com o estômago embrulhado. E respondo: comer não é prova de fome. Me lembro de pessoas que comem quando estão ansiosas, deprimidas, alegres… e elas comem com mais gosto do que uma criança somaliana comeria um Big Mac. Se comer algo não é prova de fome, o que seria então uma boa prova? Testes para medir o açúcar do sangue? Algum exercício físico para ver se você apresenta sinais de fraqueza? Não isso tudo poderia trazer, na verdade com certeza traria resultados falso-positivos. Vamos tentar algo diferente então. Pense em alguém que você ama. Prove que de fato ama essa pessoa. Opsss… mesmo problema, da mesma forma que não podemos usar a fome para justificar a fome, não podemos usar o amor para justificar o amor e nem mesmo a lógica para justificar a lógica.
Bem, Gödel, em seus lampejos de genialidade que apenas a loucura consegue causar se dedicou a tentar entender isso. Como fome e amor são conceitos muito abstratos ele tentou se apegar àquilo que qualquer animal, até mesmo um humano, teria facilidade em trabalhar. Ele se apegou a números. E para não se perder neles resolveu pegar o grupo mais comum e sem graça de números, os números inteiros (lembre-se que números inteiros são todos os números naturais incluindo o zero e os números negativos, (…, -2, -1, 0, 1, 2, …). Então ele pensou que qualquer sistema axiomático – ou seja qualquer conjunto de axiomas que podem ser usados para se derivar logicamente qualquer teorema – que possa ser criado para se incluir a aritmética dos números inteiros, ou seja um sistema formado por hipóteses iniciais de onde se derivam enunciados que tem a ver com as possíveis operações matemáticas que envolvam o grupo dos números inteiros não pode ser ao mesmo tempo nem completo e nem consistente.
Coisa de louco né?
Sim, literalmente coisa de louco, Gödel não ia aos hospícios para se bronzear. Tecnicamente o que ele falou, em linguagem de pessoas sãs, é que se um sistema tem consistência, ou seja que é estável, ele não pode ser completo, e se é completo não pode ser consistente. Se existe um sistema auto-consistente então existirão proposições que não poderão ser nem comprovadas nem negadas por esse mesmo sistema (ele é incompleto) e caso o sistema seja completo, ele não pode validar a si mesmo (seria inconsistente). Isso significa que você não pode usar a fome para comprovar a fome, que seria necessário um computador fora do universo para entender o universo, que sua língua não pode se auto-saborear e que nós nunca poderemos provar que 2+2=4.
“E por que isso é interessante?” você se pergunta, “por que estou perdendo tempo com isto?”
Vamos começar do básico. Quando disse que não podemos provar que 2+2=4 não quero dizer que você não é capaz de colocar duas bananas na sua frente ao lado de duas pêras e contar que tem quatro frutas. Como dissemos até macacos fazem isso. Mas deixe as frutas de lado e pegue um lápis e um papel e pense no passado. Quando você era uma criancinha, seus professores adoravam abusar de você com tabuadas. Tabuadas de soma, de subtração, de divisão de multiplicação. Se hoje você consegue responder rápido quanto é 5×4 ou 11+3 não é porque saiba calcular, mas é porque decorou. Veja que responder quanto é 7×8 ou 11.347+32 não é tão rápido, apesar de serem contas tão fáceis quanto essas primeiras. Esse condicionamento desde criança serviu para que algumas verdades absolutas fossem colocadas em sua cabeça, assim desde criança você acredita que 2+2 é igual a 4. Mas será que é mesmo? Vejamos, pense em um exemplo da vida real em qeu você lide com números negativos. Qualquer pessoa que já tenha tido ou que tenha um cartão de crédito acha essa fácil. Pense em uma situação onde você lide com frações. Qualquer pessoa que tenha pedido uma pizza para 2 ou mais pessoas também se sai bem dessa. Agora pense em uma situação onde você tenha que lidar com a multiplicação de frações negativas. Onde isso entra no seu cotidiano? Chega uma hora que a coisa só faz sentido no papel.
Então você tem como provar que 2 + 2 = 4. Tem a matemática para isso. Da mesma forma você pode provar matematicamente que isso pode ser provado matematicamente. Não apenas isso, mas podemos provar que é possível provar que é possível provar que 2 + 2 = 4. E isso também pode ser provado.
Agora 2 + 2 não é 23. E nós podemos provar matematicamente que 2 + 2 não é 23. E podemos provar que podemos provar que 2 + 2 não é 23. E podemos provar que podemos provar que podemos provar isso. E isso também pode ser provado.
Assim pode ser provado que 2 + 2 não é 23. Mas poderia ser provado também que 2 + 2 é 23? Parece uma pergunta idiota, mas é algo crucial. Se for possível provar isso onde nossos professores de matemática se esconderiam de vergonha? Seria algo devastador, pois se for possível provar que 2 + 2 = 23, então seria possivel provar que 23 não é 23, pois também podemos provar que 2 + 2 não é 23. Isso significara que não existe nada que não pudesse ser provado, e isso é apenas uma outra forma de dizer que nada é verdadeiro e portanto tudo é permitido e então todas as nossas certezas seriam meras apostas mais ou menos convenientes.
Ficando confuso? Vou escrever mais devagar então para você tentar acompanhar.
Neste ponto devemos nos perguntar: Existe uma forma de provarmos que não pode ser provado que 2 + 2 = 23?
Claro que você já deve ter imaginado a resposta chocante de Gödel. Não apenas não podemos, como também jamais poderemos. Mais ainda: se pode ser provado que nunca provaremos que 2 + 2 = 23 então que base temos para afirmar qualquer coisa logicamente? E se nenhum argumento do tipo “prove que X não pode ser provado” pode ser provado então sabemos que a lógica e a matemática são tão inconsistentes quando qualquer outra forma de crença.
Gödel nos mostrou que não podemos entender o universo se fazemos parte do universo, que não podemos compreender a vitamina que estamos fazendo se estamos presos dentro do liquidificador. Para isso seria necessário que uma mente ou um computador de fora de nosso universo nos analisasse. E você achava engraçado aquele papo de 42 e a pergunta correta não poderem co-existir na mesma realidade, tsc, tsc…
Agora, isso tudo seria já um papo interessante de bar se parasse por ai, mas lembre-se do começo do texto: Gödel costumava ser institucionalizado. Em hospícios. Logo, tudo isto apenas serve para o próximo passo lógico – se é que você ainda acredita nessa superstição que chamamos “lógica”.
Embora não se possa ser provado que não pode ser provado que 2 + 2 = 23, podemos provar que se pode ser provado que não pode ser provado que 2 + 2 = 23. Então podemos provar que 2 + 2 = 23. Ou seja, se pudesse ser provado que não pode ser provado que 2 + 2 = 23 então também poderia ser provado que 2 + 2 é 23!
Confuso não? Mas este não é um problema da sua capacidade de compreensão mas sim um problema da compreensão de nossa capacidade. Na verdade o que o bom e velho Kurt fez foi expressar matematicamente o antigo paradoxo da auto-referência historicamente atribuído a Epimenides. Epimenides era de Creta e dizia que todos os Cretenses são mentirosos. Isso é como ler um a placa dizendo:
“Esta frase é falsa.”
Vamos chamar essa frase de afirmação G em homenagem a Göedel. Agora pergunte a si mesmo, a afirmação G é verdadeira? Se G é verdadeiro então temos uma afirmação válida que é falsa, mas se G é falso então sua afirmação é verdadeira. Ou seja, se a frase for verdade ela é uma mentira, se ela for uma mentira então ela é verdadeira. É a mesma coisa que você pedir para o Pinocchio dizer a frase: “Agora meu nariz vai crescer!” o que acha que vai acontecer?
Isso não quer dizer que devemos abandonar a lógica e sair por ai passando Amendocrem nas genitálias das crianças, mas quer dizer que G é incompleto. O mesmo pode ser feito com qualquer outro sistema, mostrando que não apenas haverão erros que jamais poderão ser provados como sendo erros, como também haverão verdades que não poderão ser provadas. E isso não apenas na matemática. Pense em Deus, amor, na crença que chocolate é gostoso e fígado ruim, que aquilo que você acredita ser correto é realmente correto. São coisas que não poderão ser provadas ou descartadas nunca, não de uma forma que possamos compreender.
BÔNUS
Ainda não entendeu do que falamos? Pelas coxas de Maria! Sejamos explícitos então. Está com aquele lápis e o papel nas mãos?
1- Vamos começar assumindo que A e B tem o mesmo valor. A então é igual a B.
2- Vamos multiplicar ambos os lados por A.
3- Vamos agora subtrair os dois lados da equação por B elevado a 2.
4- Lembra-se da matemática do colégio? Vamos fatorar os dois lados, ou seja, ver o que eles tem em comum e separar, no caso ambos os lados tem (A-B) em comum, então fatorado fica assim.
5- Como temos (A-B) multiplicando dos dois lados da igualdade podemos dividir os dois lados por (A-B) ficando com este resultado.
6- Como afirmamos no início que A=B então A+B=B é a mesma coisa que B+B=B ou A+A=A, vamos ficar com a primeira opção. Simplificando temos que B+B é igual a B vezes 2.
7- Vamos dividir os dois lados por B agora.
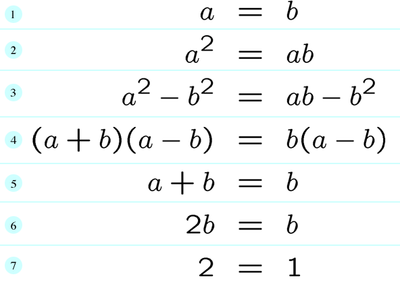

por LöN Plo
Alimente sua alma com mais:

Conheça as vantagens de assinar a Morte Súbita inc.
Faça parte do problema
Recursos Avançados
+ Área Restrita + Eventos Online.
R$37,00 por mês




